I am in the process of revising my annual lecture to first year university students on the topic of “curly arrows”. I like to start my story in 1924, when Robert Robinson published the very first example[cite]gg9g[/cite] as an illustration of why nitrosobenzene undergoes electrophilic bromination in the para position of the benzene ring. I follow this up by showing how “data mining” can be used to see if this supports his assertion. I have used the very latest version of the CSD crystal structure database to update the version originally posted here in 2020.[cite]10.59350/c6thp-wqe69[/cite]
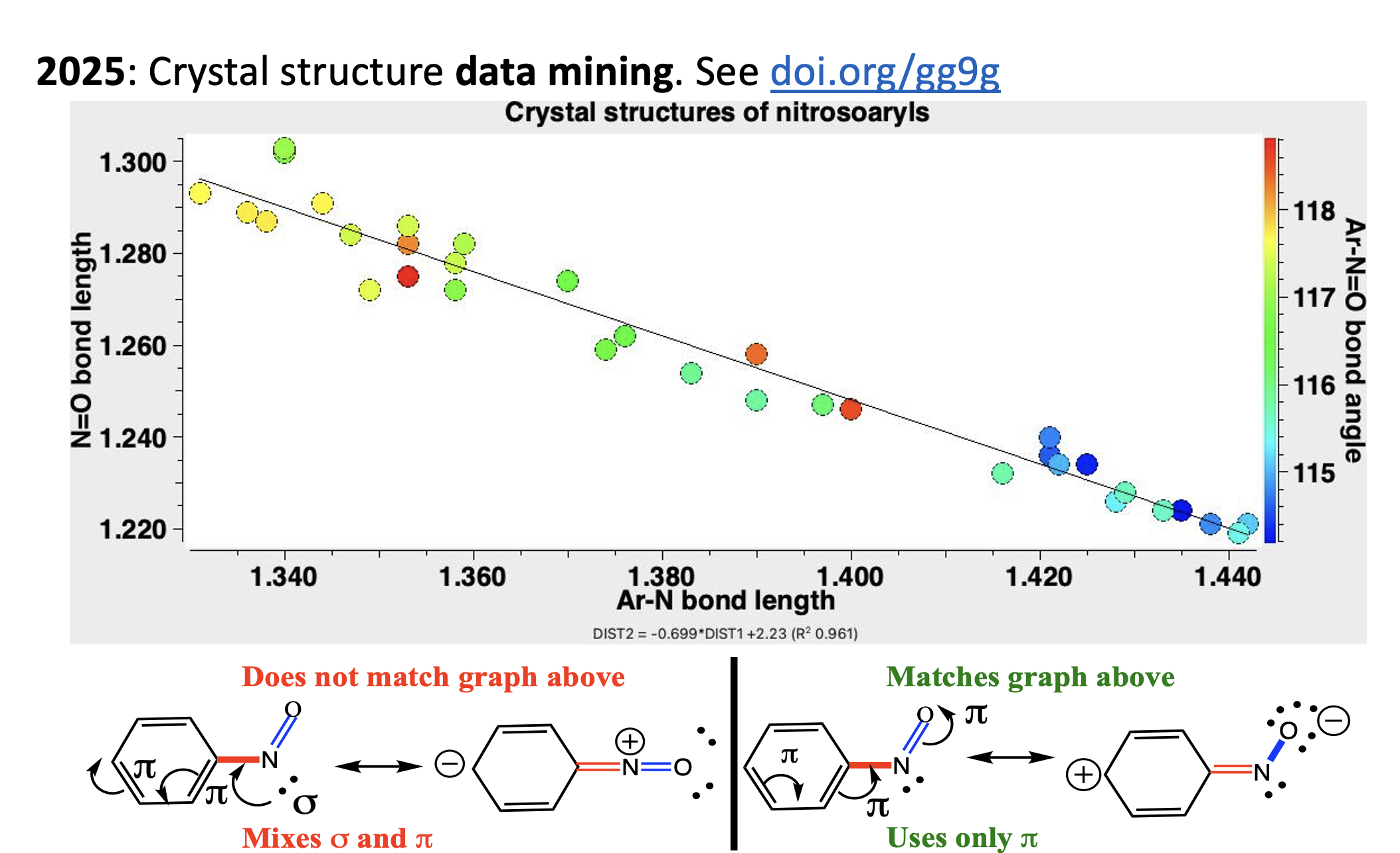
I then discuss some possible reasons why Robinson might have thought that bromination goes in the para position, including the observation[cite]10.1002/mrc.1260251118[/cite] that nitrosobenzene is in equilibrium with its dimer, and that such a dimer might be expected to more reactive towards electrophiles than the “deactivated” monomer.
Not part of the main lecture, but held in reserve for any questions at the end, is the following curly arrow pushing for the dimerisation.
This raises a simple question – do both the red and blue arrows shown below participate at the same time, or do they go sequentially? Time then for some calculation to answer this last question. An ωB97XD/Def2-TZVPP/SCRF=chloroform calculation[cite]10.14469/hpc/15278[/cite] using a closed shell wavefunction (to correspond to two-electron curly arrows) appears to show a smooth reaction profile. The N-N bond length also converges from no bond to a double bond shortly after the transition state (NN = 1.3Å) without anything intermediate (this for the (Z)-stereochemical isomer, not the one shown above and which will be discussed later). The reported activation free energy for this process ΔG198 is 15.7 kcal/mol[cite]10.1002/mrc.1260251118[/cite] whilst the calculated value by this method is 25.5 kcal/mol. Even allowing for a concentration effect (1M) and quasi-harmonic corrections to the free energy, it is still 23.9 kcal/mol.
In a previous post[cite]10.59350/k4340-t6971[/cite] when an overly large barrier was computed, one reason is that the wavefunction might have “biradical” character and that the appropriate curly arrows might not be the appropriate two electron variety at all, but instead one-electron ones, as shown below.
The degree of biradical character is given by the spin-expectation operator 2>, which has a value of 0.0 for no biradical character and 1.0 for a pure biradical. This time the transition state for the dimerisation is calculated to have a value of 2> = 0.5418 and ΔG198 is now calculated as 21.8 kcal/mol (20.3 with quasi-harmonic corrections).
The energy and N-N bond length profiles for the reaction coordinate using “one-electron” curly arrows are shown below, the former being around 4 kcal/mol lower than for the two-electron arrows.
The dihedral at the central C-N-N-C bond shows it almost entirely twisted at the transition state (as might befit a biradical) and then a smooth rotation to co-planarity (as befits a double bond) as the second bond forms.
Because the system has C2-symmetry and importantly no plane of symmetry, the π and σ electrons are now allowed to mix together and this can be seen in the two (equivalent) orbital overlap models below at the transition state, each nitrogen lone pair managing to overlap constructively (blue with purple, red with orange, click on the diagram to load the orbitals) with the N-N π* orbital of the second nitrosobenzene.
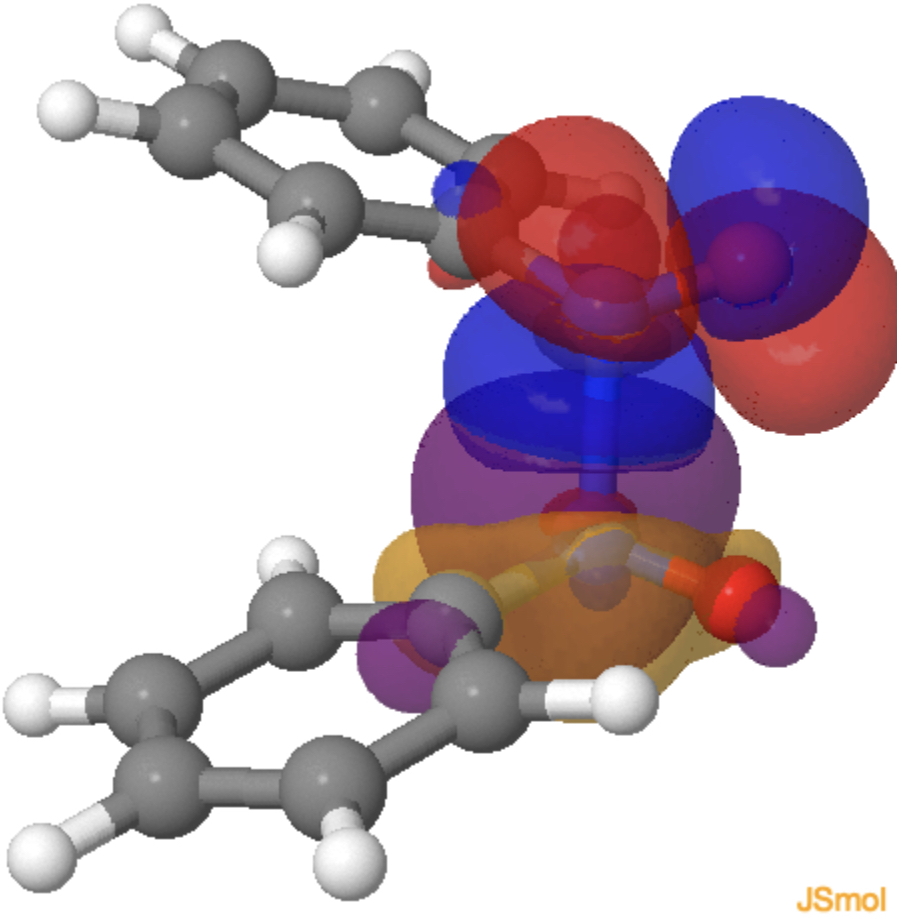
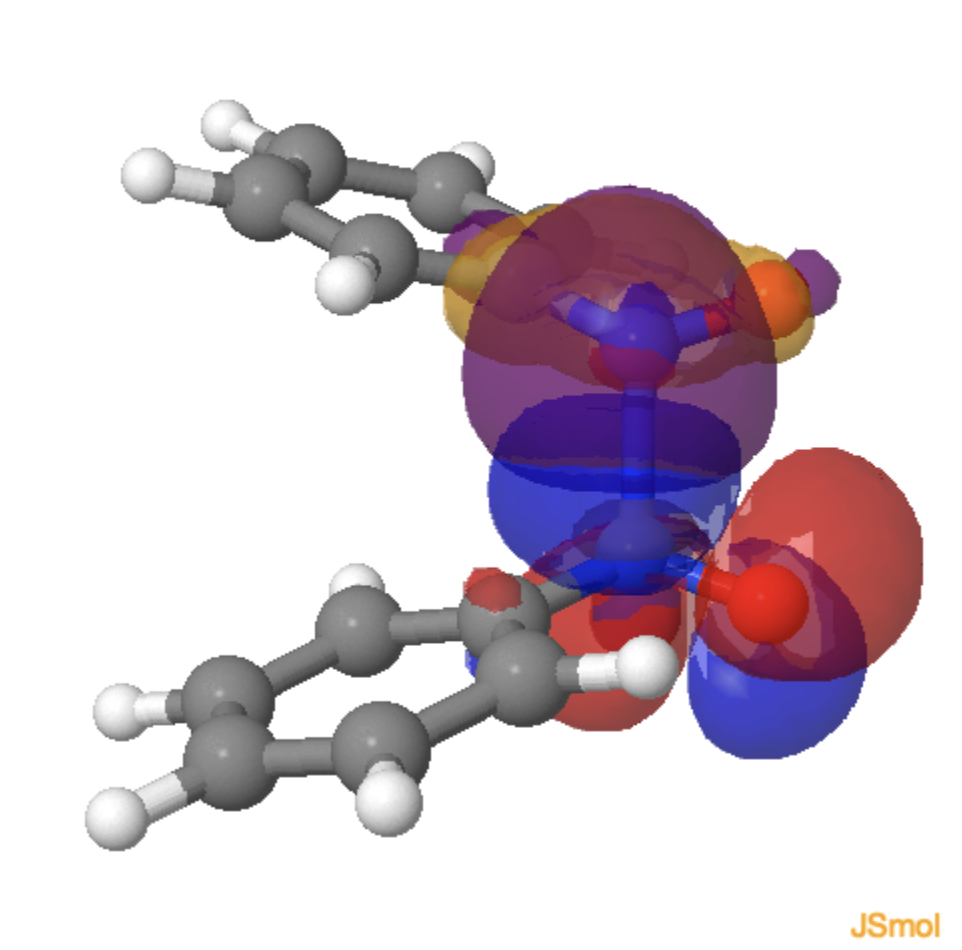
Why is this simple system better described (energetically) by the use of one-electron arrows rather than two electron ones? A simple explanation might be that the electrons like to move consecutively simply to reduce the electron repulsion that the two-electron model would impose on it (reducing the electron correlation incurred in the process). It’s probably more complicated than this, but it shows a rare example where two-electron arrows are not the most appropriate for describing a chemical reaction.
Related
You can leave a response, or trackback from your own site.

