Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The least common multiple (L.C.M.) of two or more numbers is the smallest number which can be exactly divided by each of the given number.
Least common multiple (L.C.M.) is also known as lowest common multiple (L.C.M.)
Two or more numbers may have unlimited multiples. The least of them is known as the Least Common Multiple (LCM).
Let us discuss the three methods to find the LCM of two or more numbers.
Method 1: Finding the LCM through Multiples
Working Rules for Finding the LCM through Multiples:
Step I: Find the multiples of the given numbers to such an extent, so as to obtain the smallest common multiple of the given numbers.
Step II: The smallest common multiple found in step 1 is the required LCM of the given numbers.
1. Let us find the L.C.M. of 2, 3 and 4.
Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, …… etc.
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …… etc.
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, …… etc.
Common multiples of 2, 3 and 4 are 12, 24, 36, …… etc.
Therefore, the smallest common multiple or least common multiples of 2, 3 and 4 is 12.
We know that the lowest common multiple or LCM of two or
more numbers is the smallest of all common multiples.
2. Let us consider the numbers 28 and 12
Multiples of 28 are 28, 56, 84, 112, …….
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, …….
The lowest common multiple (LCM) of 28 and 12 is 84.
3. Find the LCM of 4, 8 and 12.
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, ……
Multiples of 8 ate 8, 16, 24, 32, 40, 48, 56, 64, 72, ……
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, ……
Common multiples of 4, 8 and 12 are 24, 48, 72, ……
Lowest common multiple of 4, 8 and 12 = 24.
Therefore, the LCM of 4, 8 and 12 is 24
4. Let us consider the first six multiples of 4 and 6.
The first six multiples of 4 are 4, 8, 12, 16, 20, 24
The first six multiples of 6 are 6, 12,
18, 24, 30, 36
The numbers 12 and 24 are the first two common multiples of
4 and 6. In the above example the least common multiple of 4 and 6 is 12.
Hence, the least common multiple or LCM is the smallest
common multiple of the given numbers.
Consider the following.
(i) 12 is the least common multiple (L.C.M) of 3 and 4.
(ii) 6 is the least common multiple (L.C.M) of 2, 3 and 6.
(iii) 10 is the least common multiple (L.C.M) of 2 and 5.
The least or lowest common multiple (in short LCM) of two or more numbers is smallest number which is divisible by each of the given numbers.
4. Find the LC.M. of 12 and 18.
Solution:
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84 ……..
Multiples of 18 are 18, 36, 54, 72, 90 ………
Thus, common multiples of 12 and 18 are 36, 72,…..
There, L.C.M. of 12 and 18 is 36.
We can also find the L.C.M. of given numbers by their complete factorization.
Method 1: Finding the LCM by Factorization:
Working Rules for Finding the LCM by Factorization:
Step I: Factorize all the given numbers.
Step II: Find the product of all the factors taking maximum repetition of any factor.
1. Find the LCM of 28, 44 and 132 by prime factorization method.
Solution:
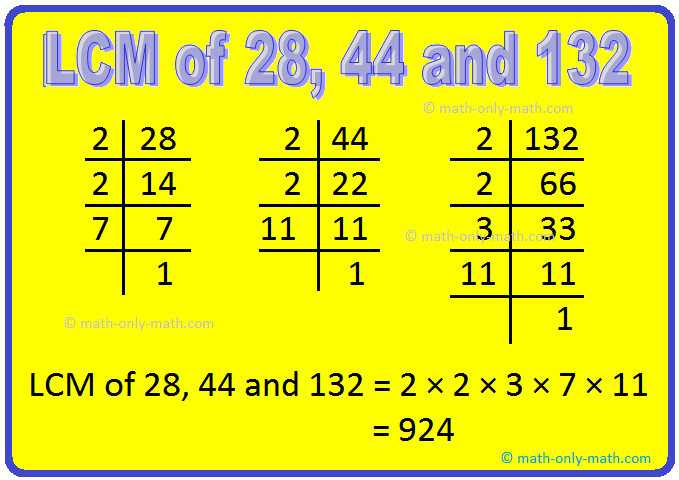
Prime factorization of 28 = 2 × 2 × 7
Prime factorization of 44 = 2 × 2 × 11
Prime factorization of 132 = 2 × 2 × 3 × 11
Here, 2 appears twice.
3, 7 and 11 appear once.
Therefore, the LCM of 28, 44 and 132 = 2 × 2 × 3 × 7 × 11 = 924
2. To find for instance, L.C.M. of 24, 36 and 40, we first factorise them completely.
24 = 2 × 2 × 2 × 3 = 2\(^{3}\) × 3\(^{1}\)
36 = 2 × 2 × 3 × 3 = 2\(^{2}\) × 3\(^{2}\)
40 = 2 × 2 × 2 × 5 = 2\(^{3}\) × 5\(^{1}\)
L.C.M. is the product of highest power of primes present in the factors.
Therefore, L.C.M. of 24, 36 and 40 = 2\(^{3}\) × 3\(^{2}\) × 5\(^{1}\) = 8 × 9 × 5 = 360
3. Find the L.C.M. of 8, 12, 16, 24 and 36
8 = 2 × 2 × 2 = 2\(^{3}\)
12 = 2 × 2 × 3 = 2\(^{2}\) × 3\(^{1}\)
16 = 2 × 2 × 2 × 2 = 2\(^{4}\)
24 = 2 × 2 × 2 × 3 = 2\(^{3}\) × 3\(^{1}\)
36 = 2 × 2 × 3 × 3 = 2\(^{2}\) × 3\(^{2}\)
Therefore, L.C.M. of 8, 12, 16, 24 and 36 = 2\(^{4}\) × 3\(^{2}\) = 144.
Method 1: Finding the LCM by Division Method:
Working Rules for Finding the LCM by Division Method:
Step I: Write all the given numbers in a line.
Step II: Think of the smallest prime number which is a factor of any of these numbers.
Step III: Divide all the numbers by this prime number obtained in step II. Remember that if any of these numbers is not divisible, retain it as it is.
Step IV: Repeat the steps II and III till you get all in the last row as 1.
1. Find the LCM of 18, 36 and 72 by division method.
Solution:
Write the numbers in a row separated by commas. Divide the numbers by a common prime number. We stop dividing after reaching the prime number. Find the product of divisors and the remainders.
So, LCM of 18, 36 and 72 is 2 × 3 × 3 × 1 × 2 × 4 = 432.
2. Find the LCM of 24, 36 and 40 by Division Method.
Solution:
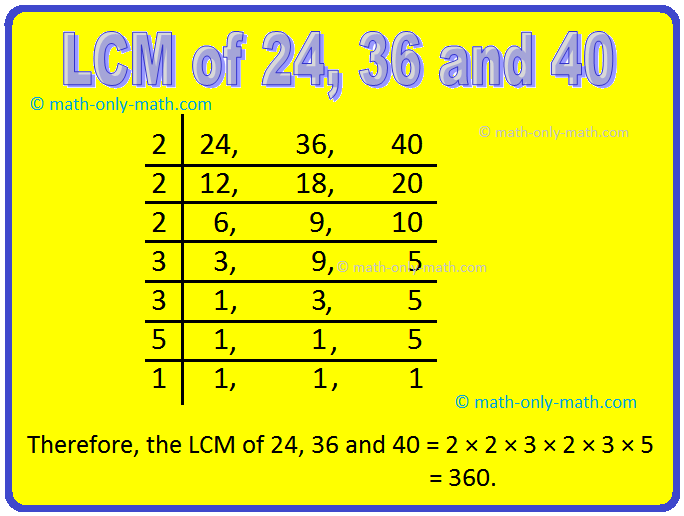
Thus, LCM of 24, 36 and 40 = 2 × 2 × 3 × 2 × 3 × 5 = 360.
LCM of Co-Prime Numbers:
LCM of the co-prime numbers is the product of the numbers.
For example:
1. Let us find the LCM of (4.9) and (3,5):

Therefore, the LCM of 4 and 9 = 4 × 9 = 36 and
the LCM of 3 and 5 = 3 × 5 = 15.
2. The LCM of two co-prime numbers is their
(a) sum; (b) difference; (c) product; (d) quotient
Solution:
It is obvious from above example that it is the product of numbers.
Therefore, the option (c) is correct.

Solved examples to find the lowest common multiple or the least common multiple:
1. Find the LCM of 3, 4 and 6 by listing the multiples.
Solution:
The multiple of 3 are 3, 6, 12, 15, 18, 21, 24
The multiple of 4 are 4, 8, 12, 16, 20, 24, 28
The multiple of 6 are 6, 12, 18, 24, 30, 36, 42
The common multiples of 3, 4 and 6 are 12 and 24
So, the least common multiple of 3, 4 and 6 is 12.
We can find LCM of given numbers by listing multiples or by
long division method.
2. Find the first two common multiples of: 4 and 10
Solution:
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ……
Multiples of 10 are 10, 20, 30, 40……
Thus, the first two common multiples of 4 and 10 are 20 and 40.
3. Find the LCM of the denominators of the fractions \(\frac{1}{2}\), \(\frac{3}{4}\), \(\frac{5}{7}\) and \(\frac{7}{9}\).
Solution:
Denominators of the fractions are 2, 4, 6 and 9.
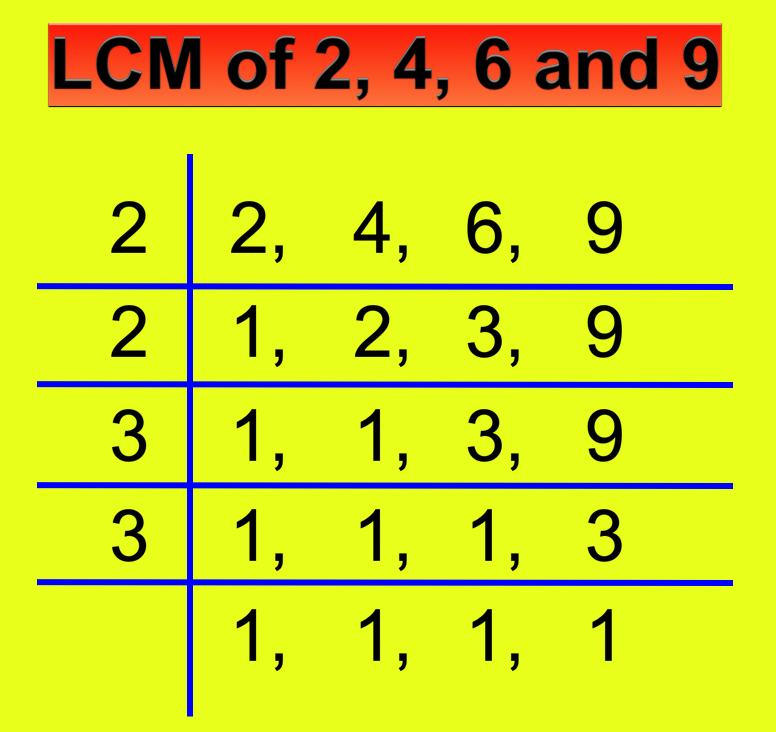
LCM of the denominators = 2 × 2 × 3 × 3 = 36.
4. Find the LCM of the denominators of the fractions \(\frac{1}{4}\), \(\frac{5}{8}\), \(\frac{7}{12}\) and \(\frac{13}{24}\).
Solution:
Denominators of the fractions are 4, 8, 12 and 24.

LCM of the denominators = 2 × 2 × 2 × 3 = 24.
Worksheet on Least Common Multiple:
I. Find the LCM of the given numbers. First one is shown
for you as an example.
(i) 3 and 6
3 = 3, 6, 9, 12, 15, 18, 21, 24, 27 ………….
6 = 6, 12, 18, 24, 30, 36, 42 ………….
The common multiples of 3 and 6 are 6, 12, 18 ………….
Lowest common multiple of 3 and 6 is 6.
(ii) 2 and 4
(ii) 4 and 5
(iii) 3 and 12
(iv) 15 and 20
Answers:
I. (ii) 4
(ii) 20
(iii) 12
(iv) 60
Answer: Two methods of finding the LCM of numbers are illustrated below:
I. Finding the LCM by the Prime Factorisation Method
The following steps are taken to find the LCM of two or more numbers:
Step 1: Express the numbers as a product of prime factors.
Step 2: Write the highest powers of each factor among all the numbers.
Step 3: The product of these factors is the LCM of the given numbers.
II. Finding the LCM by the Division Method
The LCM of numbers can be obtained by finding their common prime factors together instead of finding them separately. In this method, we arrange the given numbers in a line, in any order. We divide by a number which divides exactly at least two of the given numbers and carry forward the numbers which are not divisible. This process is repeated till no two of the given numbers are divisible by the same number. The product of the divisors and the undivided numbers is the required LCM of the given numbers.
● Multiples.
Common Multiples.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
5th Grade Math Problems
From Least Common Multiple to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.

