Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In formation of numbers we will learn the numbers having different numbers of digits.
We know that:
(i) Greatest number of one digit = 9,
Smallest number of 2 digits = 10.
(If one is added to 9, we get 9 + 1 = 10).
(ii) Greatest number of 2 digits = 99,
Smallest number of 3 digits = 100.
(If one is added to 99, we get 99 + 1 = 100).
(iii) Greatest number of 3 digits = 999,
Smallest number of 4 digits = 1000.
(If one is added to 999, we get 999 + 1 = 1000).
(iv) Greatest number of 4 digits = 9999,
Smallest number of 5 digits = 10000.
(If one is added to 9999, we get 9999 + 1 = 10000).
(iv) Greatest number of 5 digits = 99999,
Smallest number of 6 digits = 100000.
(If one is added to 99999, we get 99999 + 1 = 100000).
Thus, if 1 is added to 9 (greatest 1-digit number), we get 10 (smallest 2-digit number).
If 1 is added to 99 (greatest 2-digit number), we get 100 (smallest 3-digit number).
If 1 is added to 999 (greatest 3-digit number), we get 1000 (smallest 4-digit number).
If 1 is added to 9999 (greatest 4-digit number), we get 10000 (smallest 5-digit number).
If we add 1 to 9999, we get 9999 + 1 = 10000, the smallest 5-digit numbers.
If we add 1 to 99999, we get 99999 + 1 = 100000, the smallest 6-digit numbers.
Forming 5-Digit Numbers Video
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Forming 6-Digit Numbers Video
|
Number of Digits |
Smallest Number |
Greatest Number |
|
One |
0 |
9 |
|
Two |
10 = 9 + 1 |
99 |
|
Three |
100 = 99 + 1 |
999 |
|
Four |
1000 = 999 + 1 |
9999 |
We observe that
● The smallest 2-digit number is the
(Greatest 1-digit number + 1)
● The smallest 3-digit number is the
(Greatest 2-digit number + 1)
● The smallest 4-digit number is the
(Greatest 3-digit number + 1)
● Therefore,
The smallest 5-digit number is the
(Greatest 4-digit number + 1)
i.e., 999 + 1 = 10000 (Ten thousand)
We read 100000 as one lakh. The sixth place from the right is called lakhs place.
For Example:
500000 –> read as five lakh.
639043 –> read as six lakh thirty-nine thousand forty-three.
832519 –> read as eight lakh thirty-two thousand five hundred nineteen.
999999 –> read as nine lakh ninety-nine thousand nine hundred ninety-nine.
999999 is the greatest 6-digit number.
Look at the following table:
Now we will learn how to use
an abacus in number formation
These facts can be expressed on a spike-abacus as
follows:
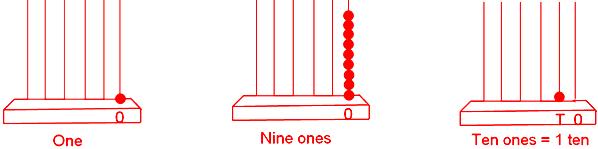
One → 9, 9 + 1 = 10 = One ten
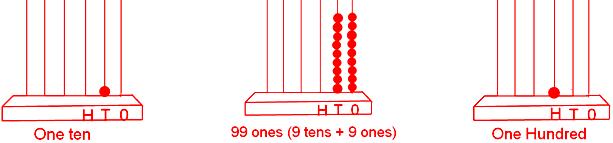
10 → 99, 99 + 1 = 100 = One hundred
100 → 999, 999 + 1 = 1000 = One thousand
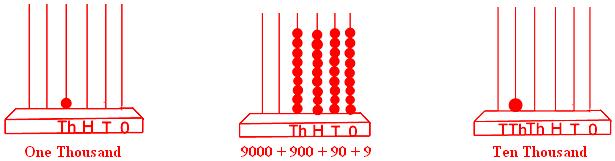
1000 → 9999, 9999 + 1 = 10000 = Ten thousand
1-digit numbers:
1, 2, 3, 4, 5, 6, 7, 8, 9.
2-digit numbers:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, …………., 29,
30, 31, ……., 39, 40, 41,……….., 49, 50, 51,………, 60, 61,………., 69, 70, 71, 72, ……….., 79, 80, 81, ………., 89, 90, 91, ……………………, 99
3-digit numbers:
100, 101, …….., 199, 200, 201, ……, 299, 300, ……., 399, 400, ………, 499,
500, ….., 599, 600, ……, 699, 700, …., 799, 800, 801, ……, 890, ……., 899,
900, 901, ………, 990, 991, ……………, 999.
4-digit numbers:
1000, 1001,……,1099,1100,1101,……,1199,1200,1201,…………,1299,
1300, ……, 1399, 1400, 1401, …….,1499, 1500, 1501,……., 1599, 1600,
1601, ….., 1699, 1700, 1701, ……, 1799, 1800, 1801,………, 1899, 1900,
1901, ……., 1999, 2000, 2001, ……., 2999, 3000, 3001, …….., 3999, 4000,
4001, ……, 4999, 5000, ……., 5999, 6000, ……, 6999, 7000, 7001, ………,
7999, 8000, 8001, ………., 8999, 9000, 9001, ……..,9999.
5-digit numbers:
10000, 10001, ……………………………………………………………, 19999,
20000, 20001, ………………………………………………………….., 29999,
30000, 30001, ………………………………………………………….., 39999,
40000, 40001, ………………, 49999, 50000, ………………………….., 59999,
60000, 60001, ……………, 69999, 70000, ……………………… ….., 79999,
80000, 80001, ……………., 89999, 90000, …………………………….. 99999
Now 6-digit numbers begin with 99999 + 1 = 100000, i.e., hundred thousand.
1. Fill in
the blanks:
(i) 1,00,000
more than 4,52,532 is …………….
(ii) 10,000,000
more than 54,928,329 is …………….
(iii)
10,00,000 less than 32,24,521 is …………….
(iv) 100,000
less than 8,482,934 is …………….
(v) 10,000
more than 99,999 is …………….
(vi) 1,000
more than 56,784 is …………….
(vii) 10,000 less
than 39,948 is …………….
Answer:
To form a number using the given digits, start placing the digits from the left and proceed towards right, i.e., from the highest place value to the lowest place value (ones place). We can o form a number with or without repeating any digit according to the given condition.
👉 If one of the given digits is zero (0), do not write it at the left-most place.
👉 To form the smallest number, first write the smallest digit (except 0) at the left-most place (i.e., at the highest place value), then write 0 (if given) at the second place from the left, then place the remaining digits in ascending order.
👉 To form the greatest number, place the given digits in descending order starting from the highest place value to the lowest place value (ones place).
Answer:
The given three digits are 5, 8 and 0.
First, we write the largest of the given digits and then place all other digits in descending order.
Thus, we get 850, which is a 3-digit number.
For forming the greatest 5-digit number using the given digits, we repeat the largest digit, i.e., 8 thrice.
Hence, the required greatest 5-digit number is 88850.
To get the smallest 5-digit number using the digits 5, 8 and 0, first write 5 followed by 0 thrice, then write 8.
Hence, the required smallest 5-digit number is 50008.
Note: Do not write 0 at the left most place.
Answer:
To get the greatest number, we arrange the digits from the largest to the smallest, i.e., 8432.
Hence, the required greatest number is 8432.
To get the smallest number, we arrange the digits from the smallest to the largest, i.e., 2348.
Hence, the required smallest number is 2348.
Therefore, Difference = 8432 – 2348 = 6084.
Answer:
Keeping the digit 9 at extreme left place, the possible numbers are 9137, 9173, 9317, 9371, 9713 and 9731, i.e., six numbers.
Keeping the digit 1 at extreme left place, the possible numbers are 1379, 1397, 1739, 1793, 1937 and 1973, i.e., six numbers.
Keeping the digit 7 at extreme left place, the possible numbers are 7139, 7193, 7319, 37391, 7913 and 7931, ie., six numbers.
Keeping the digit 3 at extreme left place, the possible numbers are 3179, 3197, 3719, 3791, 3917 and 3971, i.e., six numbers.
Hence, 24 numbers can be formed by using the digits 9, 1, 7 and 3.
Answer:
To Form the smallest 6-digit number using the four digits 3, 0, 9 and 5 (by repeating the digits), first write the smallest digit 3 (except 0) at the left-most place (here the lakhs place), then write 0 thrice, followed by the remaining digits 5 and 9 in ascending order.
Thus, the smallest 6-digit number so formed is 300059.
To get the greatest 6-digit number using the four digits 3, 0, 9 and 5 (by repeating the digits), first write the greatest digit 9 thrice starting from the left-most place (here the lakhs place), then place the remaining digits 3, 0 and 5 in descending order.
Thus, the greatest 6-digit number so formed is 999530.
Answer:
The required greatest 4-digit number 9487.
The required smallest 4-digit number 1402.
Related Concept
● Formation of Numbers.
● Finding Out the Numbers
● Names of the Numbers.
● Numbers Showing on Spike Abacus.
● 1 Digit Number on Spike Abacus.
● 2 Digits Number on Spike Abacus.
● 3 Digits Number on Spike Abacus.
● 4 Digits Number on Spike Abacus.
● 5 Digits Number on Spike Abacus.
● Large Number.
● Place Value Chart.
● Place Value.
● Problems Related to Place Value.
● Expanded form of a Number.
● Standard Form.
● Comparison of Numbers.
● Example on Comparison of Numbers.
● Successor and Predecessor of a Whole Number.
● Arranging Numbers.
● Formation of Numbers with the Given Digits.
● Formation of Greatest and Smallest Numbers.
● Examples on the Formation of Greatest and the Smallest Number.
● Rounding off Numbers.
4th Grade Math Activities
From Formation of Numbers to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
