Beyond the Tidal Bulge

Overview

That there is no tidal bulge is the key premise of this article. Upper-level oceanography undergraduates and above know this. Yet the tidal bulge is still used to portray why the Moon is receding the Earth. If there is no tidal bulge, some other explanation is in order. That other explanation uses gravitation as the driving force but does not result in a tidal bulge.

To develop that alternative explanation, this article first explains what this tidal bulge is with respect to the Moon’s recession from the Earth. The next part explains why there is no tidal bulge. Since we do have oceanic tides, there must be some other explanation for those oceanic tides. The next portions of the article describe the dynamic theory of the tides. Next, the article addresses the key underlying issues: How do the oceanic tides work, and how do the oceanic tides make the Moon recede? Finally, the article compares tidal responses in the oceans to tsunamis and tidal responses in the solid Earth.

What is the tidal bulge?

Use any search engine to find a site on why the Moon is gradually spiraling out and you will inevitably encounter a vague explanation that it’s due to tides on the Earth raised by the Moon, or a more detailed explanation based on the Earth’s tidal bulge, as portrayed in the following image.

Source: Wikipedia page on the tides

In the above image (which is intentionally exaggerated), the actions of the Moon’s gravitation on the Earth raise a pair of tidal bulges in the Earth’s oceans, one near the sublunar point, the other on the opposite side of the Earth. The Earth’s rotation also rotates the location of the tidal bulge such that the bulge closer to the Moon slightly leads the Moon (in terms of the Moon’s orbital velocity) while the other bulge slightly trails the Moon.

Both bulges exert a gravitational force on the Moon, with the closer leading bulge making the Moon accelerate while the farther trailing bulge makes the Moon decelerate. Because the leading bulge is closer to the Moon than is the trailing bulge, the gravitational influence of the leading bulge on the Moon is greater than that of the trailing bulge. The net result is to cause the Moon to accelerate, thereby taking the Moon to a higher orbit.

There is only one problem with this simple picture: There is no tidal bulge.

There is no tidal bulge

This was one of Newton’s few mistakes. Newton did get the tidal forcing function correct, but the response to that forcing in the oceans: that was completely wrong. There is no tidal bulge.

Newton’s equilibrium theory of the tides with its two tidal bulges is falsified by observation. If this hypothesis was correct, high tide would occur when the Moon is at zenith and once again at nadir, so high tides would occur 12.421 hours apart. Most places on the Earth’s oceans do have a high tide every 12.421 hours, but whether those high tides occur when the Moon is at its zenith or nadir is sheer luck. In most places, there’s a predictable offset from the Moon’s zenith/nadir and the time of high tide, and that offset is not zero.

One of the most confounding places with regard to the tides is in Newton’s own backyard. If Newton’s equilibrium theory was correct, high tide (and low tide) would occur at more or less the same time everywhere across the North Sea. That is not what is observed. At any time of day, one can always find a place in the North Sea that is experiencing high tide, and find another place in the North Sea that is simultaneously experiencing low tide. Newton’s tidal bulge theory is falsified, right in his own backyard.

As a final nail in the coffin, the tidal bulges are not observed from coastal tidal stations, from meteorological buoys on the oceans, or from space by satellites.

Why isn’t there a bulge?

Beyond the evidence, there are a number of reasons a tidal bulge cannot exist in the oceans.

The tidal bulge cannot exist because of the way water waves propagate. If the tidal bulge did exist, it would form a wave with a wavelength of half the Earth’s circumference. That wavelength is much greater than the depth of the ocean. This means the wave formed by the tidal bulge would be a shallow wave. The speed of a shallow wave at some location is approximately ##\sqrt{gd}##, where ##d## is the depth of the ocean at that location. This tidal wave could only move at the equator at 330 m/s over even the deepest oceanic trench, 205 m/s over the mean depth of 4267 m, and less than that in shallow waters. Compare this with the 465 m/s rotational velocity at the equator at mean sea level. The shallow tidal bulge wave cannot keep up with the Earth’s rotation.

The tidal bulge also cannot exist because the Earth isn’t completely covered by water. There are two huge north-south barriers to Newton’s tidal bulge, the Americas in the western hemisphere and Afro-Eurasia in the eastern hemisphere. As an example, the tides on Panama’s Pacific coast and the tides just 100 kilometers to the east on Panama’s Caribbean coast differ greatly, in both timing and form.

A third reason the tidal bulge cannot exist is the Coriolis effect. That the Earth is rotating at a rate different from the Moon’s orbital rate means that the Coriolis effect would act to sheer the tidal bulge wave apart even if the Earth was completely covered by a very deep ocean.

What others say

I’m far from alone in saying the tidal bulge doesn’t exist. For example, from these lecture notes, the page on dynamic tides rhetorically asks “But how can water confined to a basin engage in wave motion at all like the “tidal bulges” that supposedly sweep around the globe as depicted in equilibrium theory?” and immediately responds (emphasis mine) “The answer is – it can’t.”

In Affholder, M., & Valiron, F. (2001). Descriptive Physical Oceanography. CRC Press the authors introduce Newton’s equilibrium tide but then write (emphasis mine) “For the tidal wave to move at this enormous speed of 1600 km/h, the ideal ocean depth would have to be 22 km. Taking the average depth of the ocean as 3.9 km, the speed of the tidal elevations can only be 700 km/h. Therefore the equilibrium position at any instant required by this theory cannot be established.”

But there must be a tidal bulge!

Some have argued that the tidal bulge must exist as it does an amazing job at postdicting and predicting the observed accelerations of the Moon. Of course that is the case. The argument starts with an invalid assumption: That the bulge does exist. From this, it calculates the lag angle in the above image that yields the best fit between the calculated bulge-induced lunar accelerations and the calculated lunar retroreflector observations. Of course, this is a good fit as the 12.421 hour-long period induced by the bulge matches the 12.421 hour-long period that in most places dominates the ocean tides. An invalid assumption can yield good results. That does not validate the invalid assumption. The tidal bulge does not exist.

Tide generating forces

This portion of this article is what Newton did get right with respect to the oceanic tides, which is the underlying forces that drive the tides. The development below uses modern concepts; Newton used the now rarely used synthetic geometry in his Principia in part to hide the fact that he was using his newly invented calculus and in part by a desire to present his new concepts in terms in which others of his time would feel more comfortable. Newton deemed that even algebra was too new-fangled of an idea to be deemed acceptable in his time, so he used synthetic geometry and geometric arguments. I’ll instead be using modern notation, a notation that includes the Newtonian universal gravitation constant ##G## and vector, both of which postdate the Principia by a couple of centuries.

Newtonian gravity

Suppose one wants to model the gravitational effects of a gravitating body ##B## with mass ##M_B## on a small test object ##o## with mass ##m## at which the center of mass of body ##B## is located at a point ##\vec \rho## relative to the test object. Assuming body ##B## is a point mass, or acts like a point mass (i.e., a body with a radial mass distribution), then Newton’s universal law of gravitation states that the gravitational force exerted on the test object by body ##B## is
$$\vec F_{o,B} = \frac{G M_B \, m}{||\vec \rho||^3}\vec \rho\tag{1}$$
Dividing both sides of equation (1) by the test object’s mass ##m## yields the component of the acceleration of the test object toward body ##B##:
$$\vec a_{o,B} = \frac{G M_B}{||\vec \rho||^3}\vec \rho\tag{2}$$
Next, suppose that ##\vec p## is measured with respect to the center of mass of a primary gravitating body ##A## and that the vector from the centers of mass of bodies ##A## and ##B## is ##\vec r##. Once again, Newton’s law of gravitation says the component of gravitational acceleration of body ##A## toward body ##B## is
$$\vec a_{A,B} = \frac{G M_B}{||\vec r||^3}\vec r\tag{3}$$

Next, suppose that the location of the test object is expressed as a vector ##\vec p## with respect to the origin of some other body ##A##. There are many reasons to do this. For example, the test object might be a satellite orbiting the Earth, so one naturally wants to express the orbit in an Earth-centered inertial (ECI) frame. This satellite will be affected by the gravitational acceleration toward not only the Earth but also toward the Moon and the Sun (and everything else in the universe). In the case of this article, the test object is a small parcel of water at the surface of the ocean.

Newtonian gravity in an accelerating frame

In both cases (the satellite or the parcel of water) it is desirable to to express the gravitational acceleration in equation (2) but in a frame of reference centered at body ##A##. Here we run into a problem: ECI is not an inertial frame. It is instead an accelerating frame. To address this, one needs to subtract the gravitational acceleration of body ##A## toward body ##B##, equation (3), from the acceleration of the test object toward body ##B##, equation (2), to form the acceleration of the test object toward ##B## but expressed in an ##A##-centric frame:
$$\vec a_{o,B;A} = \frac{G M_B}{||\vec \rho||^3}\vec \rho \,-\, \frac{G M_B}{||\vec r||^3}\vec r\tag{4}$$
Assuming the vectors ##\vec p## and ##\vec r## are known, the vector ##\rho## is given by ##\vec \rho = \vec r – \vec p##. Substituting this into equation (4) yields
$$\vec a_{o,B;A} = \frac{G M_B}{||\vec r – \vec p||^3}(\vec r – \vec p) \,-\, \frac{G M_B}{||\vec r||^3}\vec r\tag{5}$$
Writing ##\vec p = p(\cos\theta \,\hat r + \sin\theta \,\hat t\,)## where ##p = ||\vec p||##, ##\theta## is the angle between ##\vec r## and ##\vec p##, ##\hat r## is the unit vector pointing from body ##A## to body ##B##, and ##\hat t## is the unit vector orthogonal to ##\hat r## that is in the ##A-o-B## plane, equation (5) becomes
$$\vec a_{o,B;A} = \frac{G M_B}{||(r-p\cos \theta)\hat r – p\sin\theta\,\hat t||^3}((r-p\cos \theta)\hat r – p\sin\theta\,\hat t)) \,-\, \frac{G M_B}{||\vec r||^3}\vec r\tag{6}$$

Note that if ##p\ll r##, for ##\theta## an integer multiple of 90°, the above simplifies to ##GM p/r^3## relations (to first order). This is why many say that tidal forces are inverse cube forces compared to the inverse square force of Newtonian gravity.

A graphical depiction

For points on the surface of the Earth, this results in the following image:

Source: Tidal force asymmetry @ mercer.edu

Computation

Note that equation (5) calculated naively results in significant cancelations and hence can result in significant loss of precision when performed using a computer’s native representation of the real numbers. This potential precision loss can be addressed; for example, see the book An introduction to the mathematics and methods of astrodynamics by Richard Battin, published in 1999. The focus in this book is satellites orbiting a primary body rather than parcels of water on the Earth’s surface. The mathematics are the same. Aside: In aerospace, we call these tidal gravitational accelerations third body effects as we use the term tidal gravitation to describe how the Moon and Sun distort the shape and surface of the Earth; these distortions have a gravitational effect on satellites orbiting the Earth.

What is the right model?

Note that how Newton’s notion of a tidal bulge arose easily can be seen in the above image. The tidal forces appear to act to stretch the Earth along the line between the Earth and the Moon but compress the Earth orthogonal to this line. But as noted in the introduction, this bulge does not and cannot exist. What Newton got wrong, Laplace later got right (or at least pointed in the right direction).

Laplace’s dynamic theory of the tides accounts for the issues mentioned above. The dynamic theory of the tides accounts for the fact that water is a liquid that flows, accounts for the shapes and varying depths of the oceans, accounts for friction at the bottom of the ocean, accounts for resonances, and other factors. This theory explains why it’s always high tide somewhere in the North Sea (and in Patagonia, around the coast of New Zealand, and a few other places on the Earth where tides are completely bonkers).

The dynamic theory of the tides

That water flows means it is the horizontal component of the tidal forcing functions that drive the ocean tides rather than the vertical component. Note well: “vertical” does not mean “toward the center of the Earth” in this context. It instead means “in the direction of the local inward gravitational gradient”. As an aside, there are rivers such as the Mississippi and the Mekong after the Manwan Dam that flow uphill in the sense that the distance to the center of the Earth increases. They do however flow downhill in the sense that they flow in the direction of decreasing gravitational potential energy. “Down” points in the direction a plumb bob hangs, which, thanks to the Earth’s equatorial bulge, is in most places not quite toward the center of the Earth.

The horizontal components of the tidal forcing functions combined with the Earth’s rotation and with oceanic basin depths, continental outlines, and resonances result in amphidromic systems. There are points on the surface, “amphidromic points”, that experience no tides, at least with respect to one of the many frequency responses to the tidal forcing functions. The tidal responses rotate about these amphidromic points. I’ll address amphidromic systems in detail later on.

Dynamic theory of the tides developers

It helps to look at things from the perspective of the frequency domain. (Note that frequency domain analyses postdate Newton, by quite a bit, and also postdate Laplace.) These frequency-based analyses were based on the dynamic theory of the tides, and also postdate Laplace by decades. In addition to Laplace, key contributors to this overall theory include

• William Thomson (Lord Kelvin), who applied Fourier analysis to historical tidal data;
• George Darwin (Charles Darwin’s son), extended Thomson’s work. He worked with then-available models of the Moon’s orbit and gave symbols and names (e.g, M₂, the principal lunar semidiurnal tide) to the various harmonic components; and
• A.T.Doodson, who beginning in 1919 applied a newer model of the Moon’s orbit and extended the frequency analysis even further. He found 388 harmonic components, and because this is such a huge number developed a numbering scheme for the tidal components, the Doodson numbers.

Tidal harmonic components

There are a large number of frequency responses to the overall tidal forcing functions; even more components have been found since Doodson’s time.  I’ll go over just a few of these.

• The Moon is the dominant force with regard to the tides. This makes the Moon raise tides at most places on the Earth at a frequency of 1 cycle per 12.421 hours. This is the M₂ tidal frequency.
• The second largest frequency response in most places is the 1 cycle per 12 hours due to the Sun, the S₂ tidal frequency. In general, tides raised by the Sun are about half as strong as tides raised by the Moon.
• Since the Earth’s rotational axis is not orthogonal to the line from the Earth’s center of mass to the Moon’s center of mass (or to the Sun’s center of mass), the forcing functions are not quite symmetric. In the frequency domain, this asymmetry results in 1 cycle per 24.841 hours responses, twice the period of the M₂ period. This is the M₁ tidal frequency.
• Similarly, there are also 1 cycle per 24-hour tidal responses, twice the period of the S₂ period. This is the S₁ tidal frequency.
• The Moon’s orbit around the Earth is elliptical rather than circular. The Moon’s tidal influence is reduced when the Moon is near apogee, and enhanced when the Moon is near perigee. This results in fortnightly and monthly tidal frequencies (two cycles and one cycle per anomalistic month).
• The Earth’s orbit about the Sun is also elliptical, reducing the Sun’s tidal influence when the Earth is near aphelion, and enhancing it when the Earth is near perihelion. This results in semiannual and annual tidal frequencies.
• The Moon and Sun can work together to create spring and neap tides with a frequency of two cycles per synodic month.
• And a slew of others. Each of these frequencies has its own amphidromic system.

Amphidromic systems

I’ve discussed amphidromic systems previously, but haven’t described what they are. Each tidal harmonic component has its own set of amphdromic systems. An amphdromic system comprises a central amphdromic point about which tides rotate. For these amphdromic systems I’ll focus on the M₂; component, but do keep in mind that each component has its own set of amphdromic systems. With regard to the North Sea, there are three M₂ tidal amphidromic systems in the neighborhood of the North Sea. This nicely explains why the tides are so very goofy in the North Sea.

M₂ amphidromic system

The M₂ component of the tides is the roughly twice-per-day response to the tidal forcing function that results from the Moon. This is the dominant component of the tides in most parts of the world. The following image shows the M₂ amphidromic points, points where there is no M₂ component of the tides. Even though these points have zero response to this component, these amphidromic points are nonetheless critical in modeling the tidal response. The white curves emanating from the amphdromic points are “cotidal lines” that represent curves along which high and low M₂ tides occur at the same time. The colors represent the amplitude of the tidal response. Note that the amplitude grows as the distance from the amphdromic point increases.

Source: Wikipedia article on tidal constituents

Amphidromic system temporal responses

The next image, an animated gif, shows the response to the M₂ forcing over time.

Source: archived from http://volkov.oce.orst.edu/tides/global.html.

The M2 tidal response in the North Sea

I mentioned the North Sea multiple times in my response. The North Atlantic is where 40% of the M2 tidal dissipation occurs. The North Sea is a hub of this dissipation. Tides in the North Sea are crazy! There are two M₂ amphidromic points in the North Sea plus a partial M₂ amphidromic point near the tip of Norway. This explains the crazy tides in the North Sea. The image below depicts the M₂ cotidal lines in red and curves of equal amplitude in blue. Land is brown.

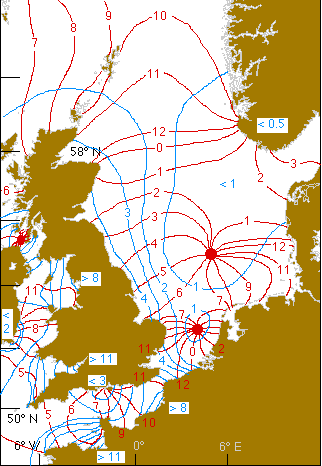
Archived source: Archived from www.geog.ucsb.edu/~dylan/ocean.html.

Energy flow of the semi-diurnal, lunar tidal wave (M2)

The image below displays the transfer of energy of the M₂ tidal from sources to sinks. This energy transfer explains the weird tides in Patagonia. Those Patagonian tides are largely a result of energy transfer from the Pacific to the Atlantic. This also shows the huge transfer of energy to the North Atlantic. 40% of the M₂ tidal dissipation occurs in the North Atlantic.

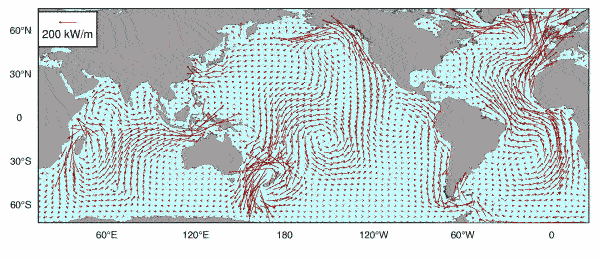
Source: Archived from www.altimetry.info/thematic-use-cases/ocean-applications/tides/.

What makes the Moon recede?

This energy transfer depicted above is closely related to the transfer of angular momentum between the mantle/crust and the oceans. One measurable effect is that the Earth’s rotation is gradually slowing down. A day used to be much shorter in duration hundreds of millions years ago than it is now. This energy transfer is also closely related to angular momentum transfer between the oceans and the Moon’s orbit. Another measurable effect is that the Moon is gradually receding from the Earth. Each amphidromic system of each tidal component participates in this transfer. The contributions from the M₂ tidal form the greatest contributor.

One can think of this energy transfer as a representing “net tidal bulge.” Or not. I prefer “or not.”

Comparison with tsunamis

First off, there’s a big difference between a tsunami and the tides. A tsunami results from nearly impulsive driving impulse such as an earthquake. The tides are the response to a never-ending cyclical driving force. That said,

• The impulse response is informative of the response to a cyclical driving force.
• Tsunamis, like the ocean tides, form a shallow wave: Both “feel” the ocean bottom regardless of depth. This affects the tsunami wave speed and influences the amphodromic systems formed by the ocean tides. Topography is much more important for both tsunamis and ocean tides.
• Tsunamis, like the ocean tides, are subject to the Coriolis effect. The effect on tsunamis is small but present. Tsunamis are short-term events relative to the Earth’s rotation rate. The Coriolis effect becomes apparent in the long-term response of the oceans to a tsunami. The effect on ocean tides is to contribute to the shape and extent of the various amphidromic systems.

The link that follows provides an animation of the 2011 Tohoku, Japan earthquake tsunami.

References for the above:

Dao, M. H., & Tkalich, P. (2007). Tsunami propagation modeling? a sensitivity study. Natural Hazards and Earth System Science, 7(6), 741-754.

Eze, C. L., Uko, D. E., Gobo, A. E., Sigalo, F. B., & Israel-Cookey, C. (2009). Mathematical Modelling of Tsunami Propagation. Journal of Applied Sciences and Environmental Management, 13(3).

Kowalik, Z., Knight, W., Logan, T., & Whitmore, P. (2005). Numerical modeling of the global tsunami: Indonesian tsunami of 26 December 2004. Science of Tsunami Hazards, 23(1), 40-56.

Comparison with Earth’s solid body tides

The Moon and Sun also raise tides in the solid Earth. These are called Earth tides or solid body tides. I’ll use the latter term as these tides occur on other terrestrial bodies. Waves propagate differently in solids compared to liquids. The core-mantle boundary is much deeper than are the oceans. These differences make an equilibrium tide model a reasonable fit for the Earth’s solid body tides.

The Earth’s solid body tides and oceanic tides can thus be out of sync with one another. This can add to or subtract from the heights of the oceanic tides at those locations. Another possible interesting side effect is that many hypothesize that the Earth’s solid body tides can trigger earthquakes. The scientific jury remains out on this final item.

The use of the tidal bulge in oceanography

The Moon’s tidally-induced recession is far from the only concept in which the tidal bulge is invoked. Oceanographers still teach Newton’s equilibrium tide theory for a number of reasons. Newton’s theory does give a proper picture of the tidal forcing function. Moreover, many students do not understand how many places can have two tides a day. For that matter, most oceanography instructors and textbook authors don’t understand! Many oceanographers and their texts still hold that the outer bulge results from a centrifugal force. This drives geophysicists and geodocists absolutely nuts. That’s starting to change during the last twenty years or so. Some oceanography texts and websites have started teaching that gravitation alone explain the tides.

The use of the dynamic theory of the tides in oceanography

As noted early on, oceanographers know that Laplace’s theory of the tides yields a truer picture of the oceanic tides. Local astronomical tide predictions exist at many coastal sites around the world. These predictions use historical data to yield empirical location-specific allocations of properties of various tidal harmonic components. While very empirical and rather local, these allocations yield a very good match, after filtering out effects due to weather. They also provide insight into the amphidromic systems.

Summary

The driving forces of the tides are the Moon and to a somewhat lesser extent, the Sun. The Sun’s tidal influence is less than half that of the Moon. The responses in the oceans to these driving forces are best viewed in the frequency domain. This results in key harmonic frequencies. Switching then back to the spatial domain results in sets of amphidromic systems, several for each harmonic constituent. These frequency responses are key to an understanding of oceanic tides, both locally and globally. The amphidromic systems are key to a global understanding of the oceanic tides.

The tidal bulge no longer plays a role in oceanography except as a “lie to children” teaching device. Instructors (and some texts) quickly inform ceanography students they were just taught a “lie to children”. Instructors (and most texts) teach oceanography students the more complex dynamic theory of tides forms a much better model. The  tidal bulge however remains as a “lie to graduate physics students” regarding the Moon’s recession from the Earth. It would be nice if articles on the Moon’s recession explained that this is not quite a true picture. But they don’t, at least not yet.

Author’s note: I took an eight-year hiatus from PhysicsForums, instead posting a lot on StackOverflow and later, on StackExchange. What follows is based on one of my highest-rated answers at stackexchange.com. As the copyright owner I have no qualms reproducing it here, translating from stackexchange-flavored markdown to WordPress. I also added significant enhancements.