Ab initio parametrization of a generalized Hubbard model in a molecule displaying chirality-induced spin selectivity

Molecular electronic structure

The system under investigation, PNN, exists as two enantiomers, (R)-PNN and (S)-PNN. In this work, all calculations refer to (R)-PNN (from now on simply PNN), but the discussion applies to both enantiomers. The Kekulè structure of PNN is shown in Fig. 1a, the structures of the PXX, NMI₂ and NDI fragments are shown in Fig. S1, and highlighted in different colors in Fig. 1a.

The molecular geometries of PNN and its molecular fragments were optimized using density functional theory (DFT), as described in Section “Methods”. Figure 1b shows the energies of the frontier molecular orbitals (MO) and the isosurfaces of selected MOs relevant to PXX, NMI₂, and NDI and the entire PNN molecule. In Fig. 1c the relevant MOs for PNN are depicted. These calculations were performed using the LC-ωPBE functional, as described later in this section for the time-dependent DFT (TD-DFT) calculations, with the ω parameter set to 0.196 a₀. A similar version of the b and c plots, generated using the B3LYP functional, is shown in Fig. S3. This comparison highlights the qualitative consistency of the conclusions reported in this paragraph for both functionals. Data in Fig. 1b–c reveal a clear behavior: the MOs are well localized on the different fragments of PNN and the energy levels can be safely ascribed to the separate components. This observation supports treating each fragment separately, as discussed in Sections “Model Hamiltonian” and “The role of molecular vibrations: assessing low frequency modes”. Consistent with the donor-bridge-acceptor architecture of PNN, the highest occupied molecular orbital (HOMO) is predominantly localized on the donor unit while the lowest unccupied molecular orbital (LUMO) resides on the acceptor. The chiral NMI₂ bridge can be further fragmented into two identical NMI units, so that HOMO and HOMO-1 (LUMO and LUMO+1) of NMI₂ are approximately symmetric and antisymmetric combinations of the HOMOs (LUMOs) of interacting NMI fragments, as illustrated in detail in Section “Frontier orbitals of NMI and NMI2” of the Supporting Information.

Optical absorption spectra of PNN, PXX, NDI and NMI₂ collected in toluene at 295 K are reported in ref. ⁷ and offer the opportunity to validate the picture emerging from first principle calculations. To such an aim, we performed gas phase TD-DFT calculations (Tamm-Dancoff approximation) on PXX, NMI₂, and NDI fragments, as well as on PNN. To predict a wide range of states, including localized and charge-transfer states, we employ the optimally-tuned range-separated hybrid functional LC-ωPBE. In this functional the amount of the exact exchange varies with the interelectronic distance, as defined by a range separation parameter, ω, which is optimized for each system at hand as described in ref. ¹⁸, to best simulate ionization potential and electron affinity. A detailed comparison of our simulations with experimental data is provided in Section “TD-DFT calculations” of the Supporting Information, highlighting the excellent agreement achieved, with errors in the predicted transition energies ranging from 0.03 eV to 0.26 eV for the molecular fragments. More to the point, the PNN experimental spectrum can be safely rationalized as the superposition of the absorption spectra of the PXX, NMI₂, and NDI fragments. This result, fully confirmed by TD-DFT calculations, strongly supports the fragmentation of the PNN molecule discussed above, relying on the MO analysis.

Model Hamiltonian

Recent developments suggest that electron correlations beyond mean-field play a major role in CISS^{12,13,15,19,20}, thus limiting the applicability of mean-field approaches, including the Hartree-Fock and DFT methods. The Hubbard model^21,22,23 and the analogous Pariser-Parr-Pople model in the chemistry community^24,25 have been successfully adopted to account for strong electron correlations in many different systems, including molecular crystals^26,27, conjugated polymers²⁸, π-conjugated dyes^29,30, stable radicals^31,32, and molecular nanomagnets^33,34,35. Recently, Chiesa et al.¹⁵ proposed a Hubbard model for electron transfer through a chiral bridge, that yields sizable spin polarization in a photoexcited charge transfer system. The model accounts for nearest neighbor hopping, next-nearest neighbor SOC and strong on site electron-electron correlation with very large U/t ratio for best results. A reliable parametrization of the Hubbard model is therefore needed to validate CISS models. In this section, we propose an original strategy for the ab initio parametrization of a generalized Hubbard model for molecular systems that can be decomposed into (nearly) disjoint fragments, allowing for the assignment of individual site orbitals to each fragment. We illustrate this strategy using the chiral bridge, NMI₂ (Fig. S1 and Fig. 1a), given its significance in CISS, as discussed in ref. ¹⁵. For our purpose, the NMI₂ is divided into two equivalent fragments, each representing a distinct NMI unit and corresponding to a site in the Hubbard model (Fig. 2). On each unit, only two MOs are accounted for, a good approximation for the system at hand. The proposed approach is however more general and can be extended to address larger active spaces (Eq. S1). Hence, we propose a generalized Hubbard model describing NMI₂ in terms of two identical sites, each bearing two site orbitals as schematically shown in Fig. 2. The relevant Hamiltonian reads:

where the upper case indices run on the two sites, lower case indices run on site orbitals, and σ is the spin label, so that \({\hat{c}}_{Ii\sigma }^{{{\dagger}} }\), \({\hat{c}}_{Ii\sigma }\) and \({\hat{n}}_{Ii\sigma }\) are the creation, annihilation, and number operators for the σ-spin electron in the i-th spatial orbital of the I-th site. Barred indexes indicate the other possible value for the site, orbital or spin. The first line in Eq. (1) collects the one-electron terms of the Hamiltonian, where ϵ_i is the energy for the i-th site orbital (equal on both fragments), and t_ij is the hopping integral between the i-th and j-th orbitals (on different fragments, on-site hopping integrals do vanish). The second and third lines of Eq. (1) collect the on-site two electron terms, with U_ij measuring the repulsion between two electrons residing on the same site in the same or in different orbitals, and J_ij is the on-site exchange coupling. The fourth line of Eq. (1) describes inter-site electrostatic interactions. The fifth line in Eq. (1) introduces exciton coupling, a two-electron term that describes the interaction between on-site transition dipole moments, parameterized by the exciton coupling energy J^(exc). This term does not appear in the standard versions of the Hubbard model, but should be accounted for when several orbitals are present on each site. The derivation of this term and its relevance are discussed in the Section “Exciton coupling in Hubbard-like models” of the Supporting Information.

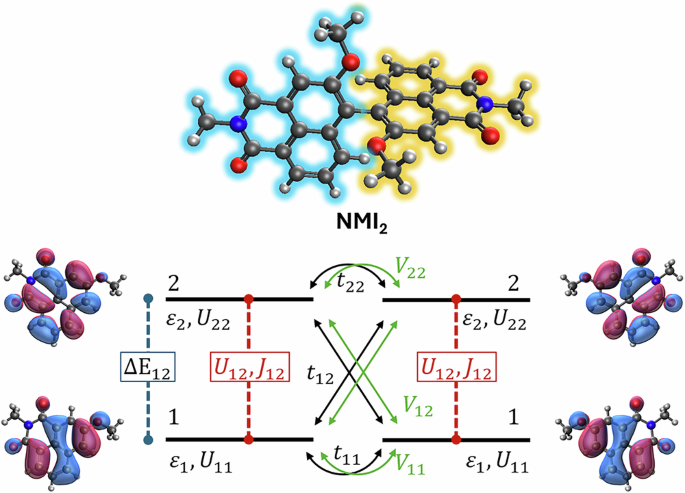
Schematic representation of the Hubbard-like model for NMI₂, described in Eq. (1), and HOMO and LUMO orbitals of NMI fragments, labeled 1 and 2, respectively.

For the parametrization of the Hubbard Hamitonian, we rely on the complete active-space configuration interaction (CASCI) approach, widely adopted as a starting point for more refined computational techniques, such as RASCI and CASSCF. CASCI offers several advantages, such as size-insensitivity and comparatively well-behaved potential energy surfaces³⁶. Moreover, it was successfully adopted to describe electronic excitations in dimers, a problem somehow relevant for our aim³⁷. Specifically, we adopt CAS-sr-DFT, a variant of CASCI, to effectively account for dynamic correlation, by incorporating short range electron-electron interactions in a DFT framework³⁸. The basis set for the CASCI and CAS-sr-DFT approaches are the electronic configurations, i.e., the states obtained populating the active orbitals with the proper number of electrons. The CASCI or CAS-sr-DFT eigenstates are obtained upon diagonalization of the relevant Hamiltonian matrix, that explicitly accounts for one- and two-electron terms. Specifically, in CAS-sr-DFT a range separation parameter is defined (we set it to 0.2 a₀ to best fit the experimental excitation energy of NMI) on the electron-electron distance, so that two-electron terms are calculated using DFT in the short range and wave function theory in the long range. Additional computational details can be found in Section “Additional results” of the Supporting Information, together with calculations for a larger active space including additional virtual orbitals (Table S10).

We adopt CAS(2,2)-sr-DFT calculations to describe each NMI fragment, i.e., including two orbitals, the HOMO and LUMO, and two electrons in the active space. Analogously, NMI₂ is described in CAS(4,4)-sr-DFT, accounting for 4 orbitals, HOMO-1, HOMO, LUMO and LUMO+1, and 4 electrons. As a first step, we run an HF calculation (6-31G(d) basis set) on the isolated NMI fragment and on a NMI ⋯  NMI system, corresponding to two NMI fragments set to a large distance ( ~ 20 Å). This procedure allowed us to verify that the pair-degenerate canonical orbitals of NMI ⋯  NMI do coincide with the canonical orbitals of the isolated NMI, so that all intersite interactions can be safely neglected in the NMI ⋯  NMI pair. The energy of the configurations E_i (the basis state of the CAS-CI calculation) can be obtained rotating the eigenvalues of a CAS(4,4)-sr-DFT calculation on NMI ⋯  NMI on the configuration basis, as follows:

where i and a run on the configurations and eigenstates, respectively, c_ia is an element of the eigenvector matrix, and ϵ_a is the a-th CAS-CI eigenvalue. Once the energies of the configurations are known, the on-site parameters (U_ij, t_ij, J_ij in Eq. (1)) can be easily obtained, as described in Section “Extraction of on-site parameters” in the Supporting Information.

Inter-site model parameters (t_ij, V_ij, J ^(exc)) rely on CAS(4,4)-sr-DFT calculation on NMI₂ and are extracted adjusting the inter-site model parameters of the Hamiltonian in Eq. (1) as to best fit the ab initio transition energies, while maintaining the on-site parameters fixed to the values obtained from NMI ⋯  NMI results. Results are listed in Table 1. A good agreement is obtained in terms of the energy (RMSE of  ~0.045 eV) and of the nature of the states, estimated in terms of the weight of charge resonance states on the CAS(4,4)-sr-DFT states compared to the Hubbard states (Table S7).

Results in Table 1 show that the inclusion of the exciton coupling term in our Hamiltonian marginally affects the global quality of the fit, while it definitely improves the the description of the lowest-lying excited states (i.e., the pair of local triplet states and the pair of local singlet states), suggesting that the exciton coupling is required for a reliable description of the low energy excited states. Moreover, accounting for exciton coupling does not significantly affect inter-site parameters with the only exception of t₂₂, that goes from  ~80 meV if the exciton coupling is disregarded, to  ~30 meV if it is accounted for.

Overall, Hubbard eigenstates are a good approximation of CAS-sr-DFT eigenstates. Minor deviations can be ascribed to two main sources: (1) the MOs of NMI₂ that enter the active space in the CAS(4,4)-sr-DFT calculation are not exactly linear combination of the same on-site orbitals that enter the CAS(2,2)-sr-DFT calculation on the NMI dimer, and (2) some of the two electron integrals that enter the CASCI calculations are not included in the neglect differential overlap approximation adopted in the Hubbard model^22,23.

Eq. (1) allows to tackle the many-body nature of the states of homodimers, as needed, e.g., to address spectroscopy, however SOC interactions must be properly accounted for to describe CISS. The general expression for the one-electron SOC Hamiltonian reads:

Where i and j indexes run on site orbitals, while σ and \({\sigma }^{{\prime} }\) run on spin. Therefore the definition of the SOC operator amounts to the determination of the one-electron integrals \(\left\langle \right.i\sigma | {\hat{h}}_{SO}| j{\sigma }^{{\prime} }\left.\right\rangle\). Towards this aim, we perform a DFT calculation on NMI₂ (B3LYP/6-31G(d), ORCA package^39,40) to extract the one-electron SOC operator written on the basis of DFT orbitals. By visual inspection (Fig. S7) and relying on symmetry considerations, the NMI₂ frontier MO can be approximated as linear combinations of the NMI orbitals as follows:

where upper and lower case letters refer to the MO of NMI₂ and NMI, respectively, and a and b refer to the two NMI sites. A straightforward basis rotation then allows to obtain the desired SOC matrix elements (SOCMEs) on the basis of the NMI site orbitals. Not surprisingly, the estimated SOC values are fairly small (Fig. S5). The largest contribution to SOC is due to its component aligned along the charge transfer axis (the long axis in our reference frame). Specifically, the \(\left\langle \right.{{\mbox{lumo}}}_{a}| {\hat{h}}_{SO,z}| {{\mbox{lumo}}}_{b}\left.\right\rangle\) integral is 1.1 cm⁻¹, with a SOC-to-hopping ratio  ~0.005, a small number that is however surprisingly large for organic molecules. As expected, the information on chirality of the system is encoded in the sign of SOC, as shown in Fig. S6, where two out of the three cartesian components of SOC change in sign upon changing the enantiomer.

The role of SOC and correlation

SOC interactions, although typically weak in π-conjugated organic systems, are essential to achieve spin polarization. Often, when modeling chiral systems as Hubbard chains with one orbital per site with nearest-neighbor (NN) hopping, a next-nearest-neighbor (NNN) SOC is included^13,15,19. Historically, this approach stems from the influential model by Kane and Mele for spin polarization in graphene⁴¹. From a symmetry standpoint, purely NN SOC and hopping terms lead to spin-independent Hamiltonians, so that the introduction of a NNN term (hopping, SOC, or both) is required to achieve non-negligible spin polarization. When multiple orbitals per site are considered, like in the model presented in Section “Model Hamiltonian”, the connectivity of the hopping and SOC operators effectively leads to different channels for SOC and hopping.

While the form of hopping and SOC operators in principle may lead to non-negligible spin-polarization for the NMI₂ bridge modeled as in Section “Model Hamiltonian”, this does not guarantee that high spin polarizations can be achieved. Indeed, theoretical approaches based on single-electron models consistently failed to quantitatively reproduce experiments where high spin polarization is measured. We therefore investigate the role of correlations in our study. Diagonalizing the model  in eq. (1) with parameters in Table 1 for a system of four electrons produces a singlet ground state, where each of the two lowest-energy orbitals, localized on separate sites, is occupied by two electrons. This state is separated by a large energy gap of  ~3.1 eV from the first excited triplet (Table S7). In order to simulate PET, we should consider an additional electron coming from the photoexcited donor. This electron will travel through the empty orbitals of the bridge, since the energy gap to involve the occupied orbital is too large (comparable to Δε₂₁ as shown in Section “Assessing the role of electron-electron correlations” of the Supporting Information). Accordingly, a significant role of electron correlations in PET dynamics can be excluded, despite the large values for the two-electron terms (U_ij, J_ij, and V_ij) found for NMI₂. While electron correlations are not relevant in the NMI₂ bridge, J and U play an important role in amplifying spin polarization in systems where orbitals are degenerate or separated by small gaps¹⁵.

The role of molecular vibrations: assessing low frequency modes

Having excluded a significant role of electron correlation in PET, we therefore turn our attention to another possible source of amplified spin polarization, namely low-energy vibrational modes interacting with electrons^13,14. The important role of vibrations in the CISS effect is also suggested by the increase of spin polarization with temperature observed in some experiments⁴².

The DFT analysis of vibrational modes of PNN in its ground-state geometry shows that low energy modes primarily involve the torsional motions around the bonds between molecular fragments. Specifically, the torsion around the donor-bridge bond mainly contributes to a mode with harmonic frequency 1.2 meV, the torsion between the two NMI fragments contributes to a mode at 1.76 meV and the torsion around the bridge-acceptor bond contributes to a mode at 3.72 meV, as displayed in Fig. S8. These torsional modes are particularly relevant to PET dynamics since they modulate the conjugation between the weakly coupled units of the system, as depicted in Fig. 3. To better investigate their nature beyond the harmonic approximation, we computed variation of the energy of the system as a function of the dihedral angle, describing the relative rotation between these units. This was done through a rigid scan, where all other atomic coordinates were kept fixed at their equilibrium values. Figure 3 collects the resulting rigid energy scans for the selected three conformational modes (the same scans on a wider range are shown in Fig. S9). Torsions around the bridge-acceptor bond lead to symmetric and harmonic potential energy scans (Fig. 3c), indicating elastic behavior and fairly rigid bonds. This is probably due to strong steric repulsion between the oxygen atoms of the carbonyl groups. Conversely, the torsion between the NMI units inside the bridge, shows a marked anharmonicity and asymmetry (Fig. 3b), with the system favoring twisting towards higher angles (i.e., methoxy-groups further apart). This asymmetry clearly results from axial chirality of the NMI₂ unit. Finally, torsions around the donor-bridge bond lead a flat, anharmonic curve characterized by a double minimum (Fig. 3a and Fig. S9), indicative of significant thermal conformational disorder, suggesting that, even at low temperatures, the molecule can explore a large configurational space. This asymmetry is only apparent: the donor-bridge bond shows no axial chirality. If all possible conformers were taken into account, symmetric behavior would be recovered.

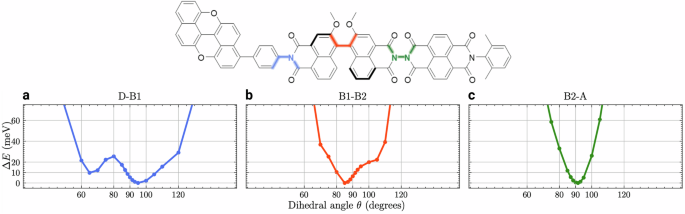
Top: The Kekulè structure of PNN with the bonds involved in the three conformational degrees of freedom are highlighted with different colors. Bottom: Rigid potential energy scans as a function of the three dihedral angles connecting the subunits of PNN: a) Donor-Bridge, b) intra-Bridge, and c) Bridge-Acceptor.

Electron-vibration coupling

Electron-vibration coupling is addressed in parametric Hamiltonians, like the generalized Hubbard model in Section “Model Hamiltonian”, selecting few relevant vibrational modes and accounting for the variation of models parameters when moving along the corresponding coordinate. In the context of site-models, like the Hubbard model or few state models for electron transfer, often one distinguishes between Holstein modes, that modulate the site energy, and Peierls modes, that modulate off-diagonal matrix elements (including the hopping integrals and the SOCMEs), while, typically, the modulation of two electron terms is neglected. For PNN, in close analogy with what observed in chemically related TADF dyes^43,44, the twists around the bond connecting two π-conjugated moieties are identified as key Peierls modes. Specifically, in the NMI₂ unit, we identify the relevant Peierls mode as the torsion around the bond connecting the two NMI units. The assessment of electron correlations presented above indicates that electron transfer through the NMI₂ bridge occurs via a single channel, with electrons hopping between the LUMOs of the NMI units. For this reason, here we obtain a preliminary estimate on the dependence of the LUMO-LUMO hopping (t_LL) and SOC (\({h}_{SO}^{(LL)}\)) on twists around the NMI-NMI bond (Fig. 4). A well-established approach to estimate the hopping integral between degenerate site orbitals relies on the same approximation as in Eq. (4), considering that LUMO and LUMO + 1 of NMI₂ are symmetric and antisymmetric combinations of the LUMOs on the NMI sites. In this approximation, t_LL is estimated as half the splitting between LUMO and LUMO + 1 of NMI₂. The reduced SOCME between LUMOs of neighboring NMI units is obtained as

where \({h}_{SO,\alpha }^{(LL)}\) is the α cartesian component of the SOCME between LUMOs of neighboring NMI units.

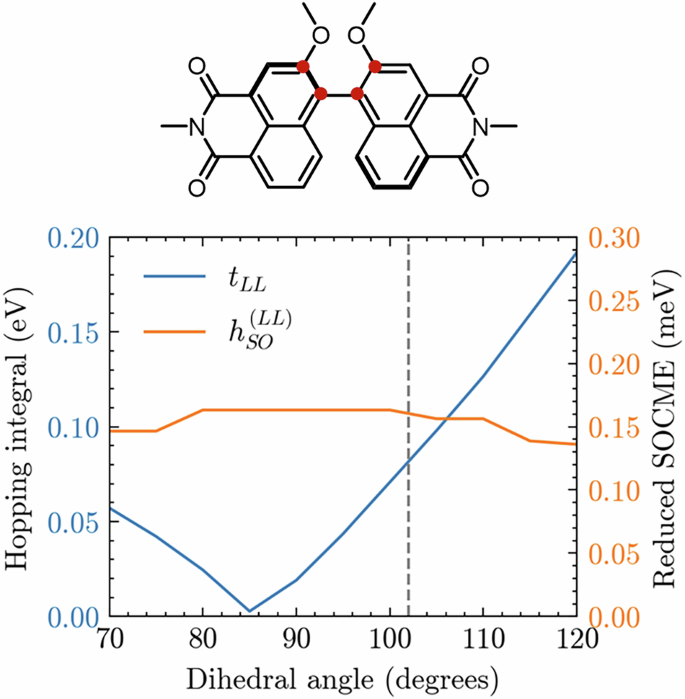
Hopping integral (blue, left y-axis) and reduced SOCME (orange, right y-axis) between on-site LUMO orbitals in the NMI₂ dimer as a function of the dihedral angle between NMI fragments. The atoms used to define the dihedral are highlighted in red in the Kekulè structure. The dashed gray line marks the value of the dihedral at the ground state equilibrium geometry.

Results in Fig. 4 show that t_LL strongly depends on the torsional mode, being almost linear in close proximity to the equilibrium geometry (~100^∘, marked in Fig. 4 with a vertical dashed line. (The equilibrium value of the dihedral is different than the one marked in Fig. 3 for the PNN complex, as here the scan is performed on the isolated NMI₂). Conversely, \({h}_{SO}^{(LL)}\) is constant over all the explored range of the torsional motion. Due to the different dependence of hopping (real) and SOC (imaginary), the phase of the total complex diabatic coupling is modulated by twists around the NMI-NMI bond. Quite interestingly, a similar modulation of the phase of the diabatic coupling was identified to lead to spin polarization in electron transport in single-channel one-electron models near conical intersections⁴⁵. While this is a promising result, it does not directly apply to the present study. Here, we explore the effects of modulation by a Peierls mode of the diabatic phase from a different perspective. Building on the conclusions of Section “The role of SOC and correlation”, we find that, upon excitation of the PXX unit, an electron is injected into the NMI₂ bridge. This reduces the problem to a single electron moving between the two LUMO levels of NMI₂. To describe this process, we consider an effective model that explicitly incorporates a torsional vibrational mode between the NMI₂ units. The Hamiltonian governing this system is given by:

where I runs on the two sites of the bridge and σ denotes the spin label. The first two terms, previously introduced in Eq. (1), now specifically describe the two LUMO levels of the bridge. The third term accounts for the electron-vibration interaction, which is modeled as a linear coupling between the electronic hopping and the nuclear coordinate \(\hat{Q}=\frac{1}{\sqrt{2}}\left({\hat{a}}^{{{\dagger}} }+\hat{a}\right)\), with \({\hat{a}}^{{{\dagger}} }\) and \(\hat{a}\) being the bosonic creation and annihilation operators, respectively. The coupling strength is determined by the parameter t₁. The fourth and fifth terms define the vibrational Hamiltonian, respectively corresponding to the harmonic oscillator Hamiltonian with frequency ω and to a quartic correction. The final two terms incorporate the SOC along z (the charge transfer direction) and x axes, respectively. The y component of the SOC is not present, as it is predicted to be zero for NMI₂ from ab initio calculations (Fig. S5 and Fig. S6). The details about the ab initio parametrization of this Hamiltonian can be found in Section “Parametrizing electron-vibration coupling” of the Supporting Information. The ab initio extracted parameters (summarized in Table S8) are ℏω = 1.52 meV, t₀= −79 meV, t₁ = −53 meV, λ_z= 0.136 meV, λ_x= 0.082 meV, ε₁ = ε₂. The quartic term k₄ serves solely as a numerical tool to confine the harmonic potential and is set to 0.1 meV.

To verify whether electron-vibration coupling alone can induce a finite in spin polarization we simulate the unitary evolution of the system starting from the initial density operator

This is a product electro-nuclear state with electrons occupying the up and down spin orbitals on site 1 with equal probability, and the void vibrational state. This unpolarized out-of-equilibrium state naturally arises from the photoexcitation of an electron into the donor LUMO, followed by an incoherent transfer to the first site of the bridge via a spin-independent jump operator of the form \({\hat{X}}_{D}={\sum }_{\sigma }{\hat{c}}_{1\sigma }^{{{\dagger}} }{\hat{c}}_{D\sigma }+h.c.\) To track the spin dynamics, we define the spin polarization operator on a site I as \({\hat{P}}_{I}={\hat{c}}_{I\uparrow }^{{{\dagger}} }{\hat{c}}_{I\uparrow }-{\hat{c}}_{I\downarrow }^{{{\dagger}} }{\hat{c}}_{I\downarrow }\). In Fig. 5, we present the time evolution of \({\langle {\hat{P}}_{I}\rangle }_{t}=Tr[\hat{\rho }(t){\hat{P}}_{I}]\) turning off (i) and on (ii) the electron-vibration coupling t₁ = 53 meV, as extracted from ab initio calculations (Section “Parametrizing electron-vibration coupling” of the Supporting Information). In the latter case, we consider both enantiomers by changing the sign of the SOC in the Hamiltonian.

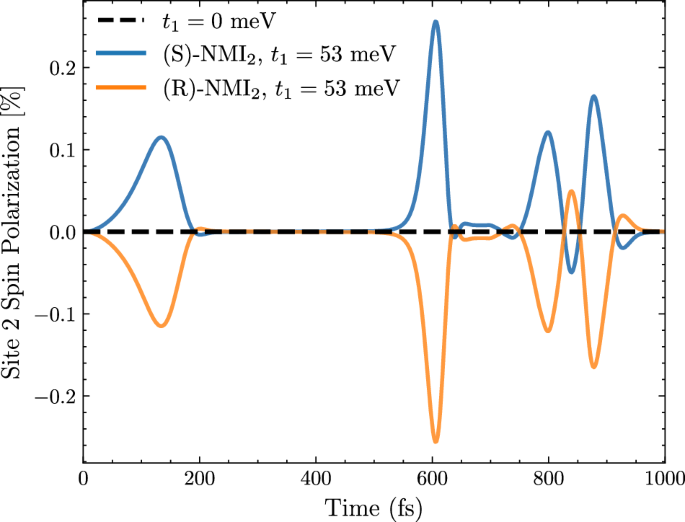
Spin polarization at site 2 of the bridge obtained from unitary time evolution over 1000 fs. The black line represents the dynamics without electron-vibration coupling, while the blue and orange lines include it with a hopping term of t₁ = 53 meV for the (S) and (R) enantiomers, respectively.

The simulations highlight the crucial role of electron-vibration coupling in the emergence of spin polarization within the CISS framework in PET. As expected, for t₁ = 0 (case i) the spin polarization is zero, because the Hamiltonian reduces to a single-channel model in which the SOC can be traced out via a gauge transformation, eventually leading to a spin-independent Hamiltonian^10,46,47,48. On the other hand, (case ii) when a Peierls mode is explicitly included, finite oscillations of the spin polarization are obtained. Moreover, changing the enantiomer reverses the sign of the spin polarization, as expected.

These findings provide key qualitative insights. Typically, models for CISS rely on a multi-channel configuration (NNN interactions or multiple orbitals per site) to break the single-channel no-go theorem and obtain spin polarization. Conversely, here we show that an analogous effect can be realized by explicitly incorporating vibronic levels and electron-vibration coupling. Indeed, in this case each site hosts multiple electro-vibrational states, as illustrated in Fig. S11. In this framework, Peierls coupling introduces non-trivial connectivity and multi-channel behavior, thus establishing oscillations in the spin polarization within the chiral bridge. This is a necessary condition for spin polarization to accumulate on the acceptor once additional incoherent relaxation pathways are introduced.

In summary, our preliminary analysis of electron-vibration coupling in the NMI₂ chiral bridge reveals that low-frequency modes strongly coupled to the electronic degrees of freedom can play an important role in the CISS mechanism in small molecules, laying the ground for future studies on the role of electron-vibration coupling in CISS.