Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
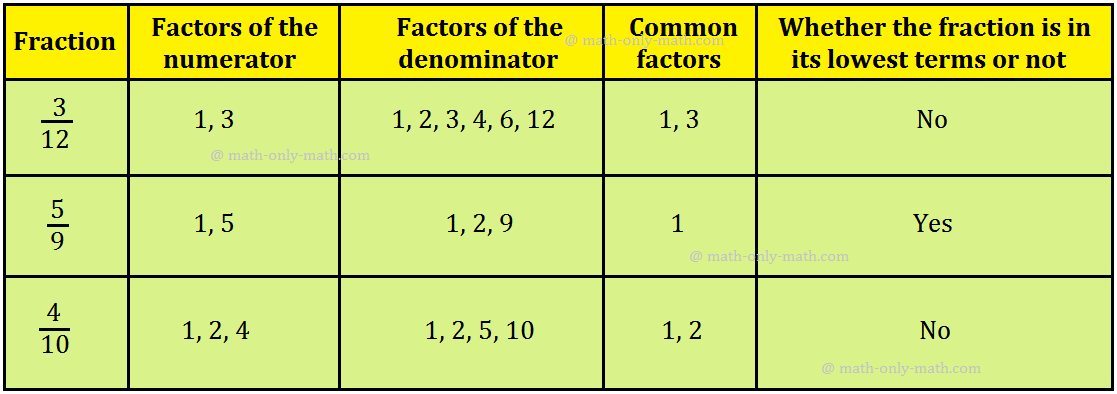
Fraction in lowest terms is discussed here.
If numerator and denominator of a fraction have no common factor other than 1(one), then the fraction is said to be in its simple form or in lowest term.
In other words, a fraction is in its lowest terms or in lowest form, if the HCF of its numerator and denominator is 1.
Definition of Fraction in Lowest Terms:
A fraction is said to be in the lowest term or the simplest form, if the HCF of numerator an denominator is 1, i.e., the numerator and denominator are not further divisible by are common number.
For example, fractions \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\), \(\frac{5}{13}\) are all in their lowest terms.
Consider the equivalent fractions:
\(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6}{9}\), \(\frac{8}{12}\), \(\frac{10}{15}\) ……..
That is , \(\frac{10 ÷ 5}{15 ÷ 5}\) = \(\frac{2}{3}\); \(\frac{10}{15}\) = \(\frac{2}{3}\)
\(\frac{8 ÷ 4}{12 ÷ 4}\) = \(\frac{2}{3}\); \(\frac{8}{12}\) = \(\frac{2}{3}\)
\(\frac{6 ÷ 3}{9 ÷ 3}\) = \(\frac{2}{3}\); \(\frac{6}{9}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\) is the simplest form of the fraction \(\frac{10}{15}\) or \(\frac{8}{12}\) or \(\frac{6}{9}\)
A fraction is in the lowest terms if the only common factor of the numerator and denominator is 1.
Observe the fractions represented by the colored portion in
the following figures.
In figure A colored part is represented by fraction \(\frac{8}{16}\).
The colored part in figure B is represented by fraction \(\frac{4}{8}\).
In figure C the colored part represents the fraction \(\frac{2}{4}\) and
In figure D colored part represents \(\frac{1}{2}\).
When numerator and denominator of fraction \(\frac{8}{16}\) are divided by 2. We get \(\frac{4}{8}\) and in the same way \(\frac{4}{8}\) gives \(\frac{2}{4}\) and then \(\frac{1}{2}\).
So, we find that \(\frac{8}{16}\), \(\frac{4}{8}\), \(\frac{2}{4}\) are equal to fraction for \(\frac{1}{2}\). Thus, \(\frac{1}{2}\) is the simplest or lowest form of all its equivalent fractions like \(\frac{2}{4}\), \(\frac{4}{8}\), \(\frac{8}{16}\), \(\frac{16}{32}\), \(\frac{32}{64}\), …… etc.
Now, if we take all the factors of the numerator 8 and denominator 16 of the fraction \(\frac{8}{16}\), we get the following:
All factors of 8 are 1, 2, 4, 8.
All factors of 16 are 1, 2, 4, 8, 16.
We find that highest common factor (HCF) of 8 and 16 is 8.
On dividing both numerator and denominator by highest common factor we get \(\frac{1}{2}\).
Since, both numerator and denominator of fraction \(\frac{1}{2}\) have no common factor other than 1, we say that the fraction \(\frac{1}{2}\) is in its lowest terms or simplest form.
A fraction is said to be in its simplest form when its numerator and denominator do not have any common factor except 1.
Observe the following:
To reduce a fraction to its lowest terms, we divide the numerator and the denominator by their common factors till only 1 is left as the common factor.
There are two methods to reduce a given fraction to its simplest form, viz., H.C.F. Method and Prime Factorization Method.
I. H.C.F. Method:
Find the H.C.F. of the numerator and denominator of the given fraction.
In order to reduce a fraction to its lowest terms, we divide its numerator and denominator by their HCF.
Example to Reduce a Fraction in Lowest Term, using H.C.F. Method:
1. Reduce the fraction \(\frac{21}{56}\) to its simplest form.
Solution:
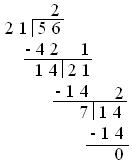
Therefore H.C.F. of 21 and 56 is 7.
We now divide the numerator and denominator of the given fraction by 7.
\(\frac{21}{56}\) = \(\frac{21 ÷ 7}{56 ÷ 7}\) = \(\frac{3}{8}\).
2. Reduce \(\frac{48}{64}\) to its lowest form.
Solution:
First we find the HCF of 48 and 64 by factorization method.
The factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
The factors of 64: 1, 2, 4, 8, 16, 32, and 64.
The common factors of 48 and 64 are: 1, 2, 4, 8, 12 and 16.
Therefore, HCF of 48 and 64 is 16.
Now \(\frac{48}{64}\) = \(\frac{48 ÷ 16}{64 ÷ 16}\)
[Dividing numerator and denominator by the HCF of 48 and 64 i.e., 16]
⇒ \(\frac{48}{64}\) = \(\frac{3}{4}\)
3. Reduce \(\frac{44}{72}\) to its lowest form.
Solution:
First we find the HCF of 44 and 72 by factorization method.
The factors of 44: 1, 2, 4, 11, 22 and 44.
The factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, and 36.
The common factors of 44 and 72 are: 1, 2 and 4.
Therefore, HCF of 44 and 72 is 4.
Now \(\frac{44}{72}\) = \(\frac{44 ÷ 4}{72 ÷ 4}\)
[Dividing numerator and denominator by the HCF of 44 and 72 i.e., 4]
⇒ \(\frac{44}{72}\) = \(\frac{11}{18}\)
To change a fraction to lowest terms:
4. Reduce \(\frac{10}{15}\) to its lowest terms:
Solution:
Step I:
Find the largest common factor of 10 and 15.
Factors of 10: 1, 2, 5, 10
Factors of 15: 1, 3, 5, 15
Common factors: 1, 5
H.C.F of 10 and 15 = 5
Step II:
Divide both the numerator and denominator by the H.C.F.
\(\frac{10 ÷ 5}{15 ÷ 5}\) = \(\frac{2}{3}\)
Therefore, \(\frac{10}{15}\) = \(\frac{2}{3}\) (in its lowest terms)
5. Reduce \(\frac{18}{45}\) to its lowest terms.
|
Solution: H.C.F. of 18 and 45 is 3 × 3 = 9 \(\frac{18 ÷ 9}{45 ÷ 9}\) = \(\frac{2}{5}\) Therefore, \(\frac{18}{45}\) = \(\frac{2}{5}\) (in its lowest terms) |
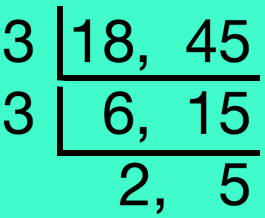 |
To express a fraction in its lowest term, we divide the numerator and denominator by their HCF.
6. Reduce these fractions in their lowest terms.
(i) \(\frac{6}{28}\)
(ii) \(\frac{24}{74}\)
Solution:
(i) In \(\frac{6}{28}\) numerator is 6 and denominator is 28.
Let us find the HCF of 6 and 28.
Factors of 6 are 1, 2, 3 and 6.
Factors of 28 are 1, 2, 4, 7, 14 and 28.
Common factors of 6 and 28 are 1 and 2.
HCF of 6 and 28 is 2.
Thus, \(\frac{6}{28}\) = \(\frac{5 ÷ 2}{28 ÷ 2}\) = \(\frac{3}{14}\)
Thus, \(\frac{3}{14}\) the simplest form or lowest term of \(\frac{6}{28}\).
(ii) In \(\frac{24}{74}\) numerator is 24 and denominator is 74.
Let us find the HCF of 24 and 74 by long division method:
24) 74 (3
– 72
2 ) 24 (12
– 24
0
HCF of 24 and 74 is 2.
Thus, \(\frac{24}{74}\) = \(\frac{24 ÷ 2}{74 ÷ 2}\) = \(\frac{12}{37}\)
Hence, \(\frac{12}{37}\) is the simplest form or lowest term of \(\frac{24}{74}\)
II. Prime Factorization Method:
Express both numerator and denominator of the given fraction as the product of prime factors and then cancel the common factors from them.
Example to reduce a fraction in lowest term, using Prime Factorization Method:
1. Reduce \(\frac{120}{360}\) to the lowest term.
Solution:
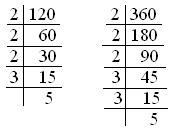
120 = 2 × 2 × 2 × 3 × 5 = 1
360 2 × 2 × 2 × 3 × 3 × 5 3
Solve Examples on Reducing Fractions to Lowest Terms:
1. Express \(\frac{28}{140}\) in the simplest form.
Solution:
Let us find all the factors of both numerator and denominator.
Factors of 28 are 1, 2, 4, 7, 14, 28
Factors of 140 are 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
The highest common factor is 28. Now dividing both numerator and denominator by 28, we get \(\frac{1}{5}\). The numerator 1 and denominator 5 have no common factors other than 1. So, \(\frac{1}{5}\) is the simplest form of \(\frac{28}{140}\).
2. Is \(\frac{48}{168}\) in its simplest form?
Solution:
Let us find HCF of numerator and denominator and then divide both by the highest common factor.
The highest common factor is 2 × 2 × 2 × 3 = 24
Let us divide both numerator and denominator by 24. We get \(\frac{2}{7}\).
So, the fraction \(\frac{48}{168}\) is not in its simplest form.
Simplifying a Fraction:
3. Simplify \(\frac{42}{84}\)
Method I:
|
Steps I: Divide numerator and denominator by 2. 42 ÷ 2 = 21; 84 ÷ 2 = 42; we get \(\frac{21}{42}\) Steps II: Divide 21 and 42 by 3. 21 ÷ 3 = 7; 42 ÷ 3 = 14; we get \(\frac{7}{14}\) Steps III: Divide 7 and 14 by 7. 7 ÷ 7 = 1; 14 ÷ 7 = 2; we get \(\frac{1}{2}\) Therefore, \(\frac{42}{84}\) = \(\frac{1}{2}\), in its lowest terms |
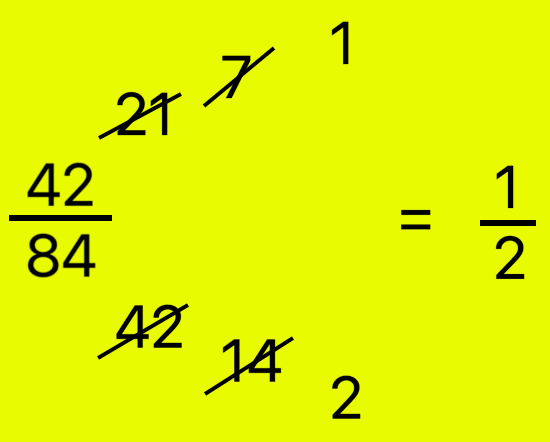 |

Simplify \(\frac{42}{84}\)
Method II:
H.C.F of 42 and 84
= 2 × 3 × 7
= 42
Now divide the numerator and denominator by the H.C.F. i.e., 42
\(\frac{42 ÷ 42}{84 ÷ 42}\) = \(\frac{1}{2}\) in its lowest terms.
4. Express each of the following fractions to its lowest terms:
(i) \(\frac{18}{27}\)
(ii) \(\frac{30}{70}\)
Solution:
(i) We have, 18 = 2 × 3 × 3
27 = 3 × 3 × 3
So, we can divide the numerator and the denominator by 3 × 3 = 9
So, \(\frac{18 ÷ 9}{27 ÷ 9}\) = \(\frac{2}{3}\)
Thus, the simplest form of \(\frac{18}{27}\) is \(\frac{2}{3}\)
(ii) We have, 30 = 2 × 3 × 5
70 = 2 × 5 × 7
So, can divide the numerator and denominator by 2 × 5 = 10
So \(\frac{30 ÷ 10}{70 ÷ 10}\) = \(\frac{3}{7}\)
Thus, the simplest form of \(\frac{30}{70}\) is \(\frac{3}{7}\)
5. Reduce \(\frac{120}{360}\) its lowest terms.
Solution:
We can divide the numerator and the denominator step by step, by their common factors.
So, \(\frac{120 ÷ 2}{360 ÷ 2}\) = \(\frac{60 ÷ 2}{180 ÷ 2}\) = \(\frac{30 ÷ 3}{90 ÷ 3}\) = \(\frac{10 ÷ 2}{30 ÷ 2}\) = \(\frac{5 ÷ 5}{15 ÷ 5}\) = \(\frac{1}{3}\)
Therefore, \(\frac{120}{360}\) equal to \(\frac{1}{3}\) its lowest terms.
Worksheet on Reducing A Fractions:
Worksheet on Reduce a Fraction to its Simplest Form:
1. Convert the given fractions in lowest form:
(i) \(\frac{2}{4}\)
(ii) \(\frac{3}{9}\)
(iii) \(\frac{4}{16}\)
(iv) \(\frac{12}{15}\)
(v) \(\frac{7}{28}\)
(vi) \(\frac{6}{10}\)
(vii) \(\frac{9}{72}\)
(viii) \(\frac{24}{36}\)
Answers:
1. (i) \(\frac{1}{2}\)
(ii) \(\frac{1}{3}\)
(iii) \(\frac{1}{4}\)
(iv) \(\frac{4}{5}\)
(v) \(\frac{1}{4}\)
(vi) \(\frac{3}{5}\)
(vii) \(\frac{1}{8}\)
(viii) \(\frac{2}{3}\)
2. Reduce the following fractions to their lowest terms.
(i) \(\frac{12}{60}\)
(ii) \(\frac{13}{169}\)
(iii) \(\frac{7}{35}\)
(iv) \(\frac{12}{28}\)
(v) \(\frac{3}{27}\)
(vi) \(\frac{80}{100}\)
(vii) \(\frac{14}{18}\)
(viii) \(\frac{29}{58}\)
(ix) \(\frac{9}{63}\)
(x) \(\frac{90}{128}\)
Answer:
2. (i) \(\frac{1}{5}\)
(ii) \(\frac{1}{13}\)
(iii) \(\frac{1}{5}\)
(iv) \(\frac{3}{7}\)
(v) \(\frac{1}{9}\)
(vi) \(\frac{4}{5}\)
(vii) \(\frac{7}{9}\)
(viii) \(\frac{1}{2}\)
(ix) \(\frac{1}{7}\)
(x) \(\frac{45}{64}\)
3. Write the fraction which is in the lowest terms in each set of equivalent fractions.
(i) [\(\frac{15}{65}\), \(\frac{3}{13}\), \(\frac{30}{130}\)]
(ii) [\(\frac{1}{9}\), \(\frac{8}{72}\), \(\frac{5}{45}\)]
(iii) [\(\frac{50}{70}\), \(\frac{5}{7}\), \(\frac{25}{35}\)]
(iv) [\(\frac{3}{11}\), \(\frac{33}{121}\), \(\frac{15}{55}\)]
Answer:
3. (i) \(\frac{3}{13}\)
(ii) \(\frac{1}{9}\)
(iii) \(\frac{5}{7}\)
(iv) \(\frac{3}{11}\)
4. State true or false:
(i) \(\frac{5}{8}\) = \(\frac{55}{8}\)
(ii) \(\frac{6}{48}\) = \(\frac{1}{8}\)
(iii) \(\frac{6}{9}\) = \(\frac{48}{75}\)
(iv) \(\frac{7}{8}\) = \(\frac{9}{10}\)
(v) \(\frac{8}{6}\) = \(\frac{28}{21}\)
Answer:
4. (i) False
(ii) True
(iii) False
(iv) False
(v) False
5. Match the given fractions:
|
(i) \(\frac{12}{15}\) (ii) \(\frac{6}{9}\) (iii) \(\frac{8}{36}\) (iv) \(\frac{24}{32}\) (v) \(\frac{15}{25}\) |
(a) \(\frac{3}{4}\) (b) \(\frac{2}{9}\) (c) \(\frac{3}{5}\) (d) \(\frac{4}{5}\) (e) \(\frac{2}{3}\) |
Answers:
5.
|
(i) \(\frac{12}{15}\) (ii) \(\frac{6}{9}\) (iii) \(\frac{8}{36}\) (iv) \(\frac{24}{32}\) (v) \(\frac{15}{25}\) |
(d) \(\frac{4}{5}\) (e) \(\frac{2}{3}\) (b) \(\frac{2}{9}\) (a) \(\frac{3}{4}\) (c) \(\frac{3}{5}\) |
6. Write the fraction for given statements and convert them
to the lowest form.
|
Statement |
Fraction |
Lowest Form |
|
(i) Ten minutes to an hour |
||
|
(ii) Amy ate 3 out of the 9 slices of a pizza |
||
|
(iii) Eight months to a year |
||
|
(iv) Kelly colored 4 out of 12 parts of a drawing |
||
|
(v) Jack works for 8 hours in a day. |
Answers:
6.
|
Statement |
Fraction |
Lowest Form |
|
(i) Ten minutes to an hour |
\(\frac{50}{60}\) |
\(\frac{5}{6}\) |
|
(ii) Amy ate 3 out of the 9 slices of a pizza |
\(\frac{3}{9}\) |
\(\frac{1}{3}\) |
|
(iii) Eight months to a year |
\(\frac{8}{12}\) |
\(\frac{2}{3}\) |
|
(iv) Kelly colored 4 out of 12 parts of a drawing |
\(\frac{4}{12}\) |
\(\frac{1}{3}\) |
|
(v) Jack works for 8 hours in a day. |
\(\frac{8}{24}\) |
\(\frac{1}{3}\) |
7. Give the fraction of the colored figure and convert in
the lowest form.
|
Figure |
Fraction |
Lowest Form |
|
|
(i) |
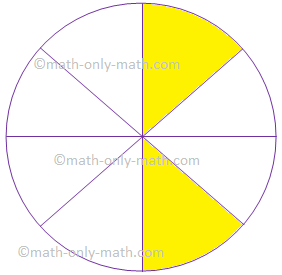 |
||
|
(ii) |
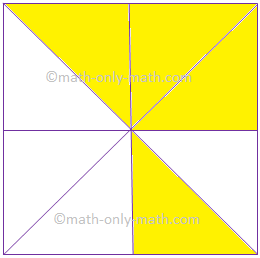 |
||
|
(iii) |
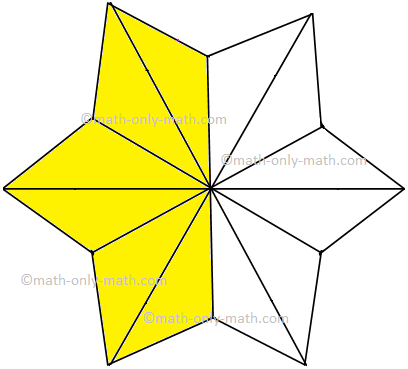 |
||
|
(iv) |
|
7.
Answers:
|
Figure |
Fraction |
Lowest Form |
|
|
(i) |
 |
\(\frac{2}{8}\) |
\(\frac{1}{4}\) |
|
(ii) |
 |
\(\frac{4}{8}\) |
\(\frac{1}{2}\) |
|
(iii) |
 |
\(\frac{6}{12}\) |
\(\frac{1}{2}\) |
|
(iv) |
|
\(\frac{2}{6}\) |
\(\frac{1}{3}\) |
8. Simplify the following fractions:
(i) \(\frac{75}{80}\)
(ii) \(\frac{12}{20}\)
(iii) \(\frac{25}{45}\)
(iv) \(\frac{18}{24}\)
(v) \(\frac{125}{500}\)
Answer:
8. (i) \(\frac{15}{16}\)
(ii) \(\frac{3}{5}\)
(iii) \(\frac{5}{9}\)
(iv) \(\frac{3}{4}\)
(v) \(\frac{1}{4}\)
9. State whether the fraction is in its lowest terms or not:
(i) \(\frac{12}{20}\)
(ii) \(\frac{8}{9}\)
(iii) \(\frac{20}{29}\)
(iv) \(\frac{5}{8}\)
(v) \(\frac{38}{57}\)
(vi) \(\frac{33}{38}\)
(vii) \(\frac{70}{95}\)
(viii) \(\frac{18}{27}\)
Answer:
9. (i) No
(ii) Yes
(iii) Yes
(iv) Yes
(v) No
(vi) Yes
(vii) No
(viii) No
10. Reduce to the lowest terms:
(i) \(\frac{10}{20}\)
(ii) \(\frac{21}{35}\)
(iii) \(\frac{36}{42}\)
(iv) \(\frac{45}{60}\)
(v) \(\frac{36}{54}\)
(vi) \(\frac{28}{49}\)
Answer:
10. (i) \(\frac{1}{2}\)
(ii) \(\frac{3}{5}\)
(iii) \(\frac{6}{7}\)
(iv) \(\frac{3}{4}\)
(v) \(\frac{2}{3}\)
(vi) \(\frac{4}{7}\)
Answer: A fraction is said to be in its lowest terms or simplest form, if its numerator and denominator do not have any common factor other than 1.
Method I:
To reduce a fraction to its lowest terms, write the numerator and the denominator in the prime factors form and cancel the common factors.
For example:
\(\frac{12}{18}\) = \(\frac{2 × 2 × 3}{2 × 3 × 3}\) = \(\frac{2}{3}\)
\(\frac{28}{49}\) = \(\frac{2 × 2 × 7}{7 × 7}\) = \(\frac{4}{7}\)
A fraction whose numerator and denominator cannot be made smaller is said to be in its lowest terms.
Method II:
To reduce a fraction into its lowest terms, divide the numerator and the denominator by their HCF.
For example:
Let us reduce \(\frac{18}{27}\) to its lowest terms.
In \(\frac{18}{27}\) numerator = 18 and denominator = 27.
Prime factors of 18 = 2, 3 and 3
Prime factors of 27 = 3, 3 and 3
HCF = 3 × 3 = 9
Therefore, \(\frac{18}{27}\) = \(\frac{18 ÷ 9}{27 ÷ 9}\) = \(\frac{2}{3}\).
Answer: We have \(\frac{126}{210}\)
Prime factorisation of 126 = 2 × 3 × 3 × 7
Prime factorisation of 210 = 2 × 3 × 5 × 7
HCF of 126 and 210 = 2 × 3 × 7 = 42
Therefore, \(\frac{126}{210}\) = \(\frac{126 ÷ 42}{210 ÷ 42}\) = \(\frac{3}{5}\)
Hence, \(\frac{126}{210}\) in its lowest terms is \(\frac{3}{5}\).
Answer: We have \(\frac{56}{84}\)
HCF of 56 and 84 = 28
Therefore, \(\frac{56}{84}\) = \(\frac{56 ÷ 28}{84 ÷ 28}\) = \(\frac{2}{3}\)
We can’t simplify further.
Hence, \(\frac{2}{3}\) is the lowest form of \(\frac{56}{84}\).
● Fractions
Fractions
Types of Fractions
Equivalent Fractions
Like and Unlike Fractions
Conversion of Fractions
Fraction in Lowest Terms
Addition and Subtraction of Fractions
Multiplication of Fractions
Division of Fractions
● Fractions – Worksheets
Worksheet on Fractions
Worksheet on Multiplication of Fractions
Worksheet on Division of Fractions
7th Grade Math Problems
From Fraction in Lowest Terms to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.

