Cyclo-S6 (Hexathiane) – anomeric effects again!
I thought I was done with exploring anomeric effects in small sulfur rings. However, I then realised that all the systems that I had described had an odd number of atoms and that I had not looked at any even numbered rings. Thus hexasulfur is a smaller (known) ring version of S8, the latter by far the best known allotrope of this element of course.
Its crystal structure[cite]10.1515/znb-1978-1238[/cite] shows it has D3d symmetry, with six identical S-S bond lengths of 2.068Å. A MN15-L/Def2-TZVPP calculation[cite]10.14469/hpc/15261[/cite] replicates this pretty well.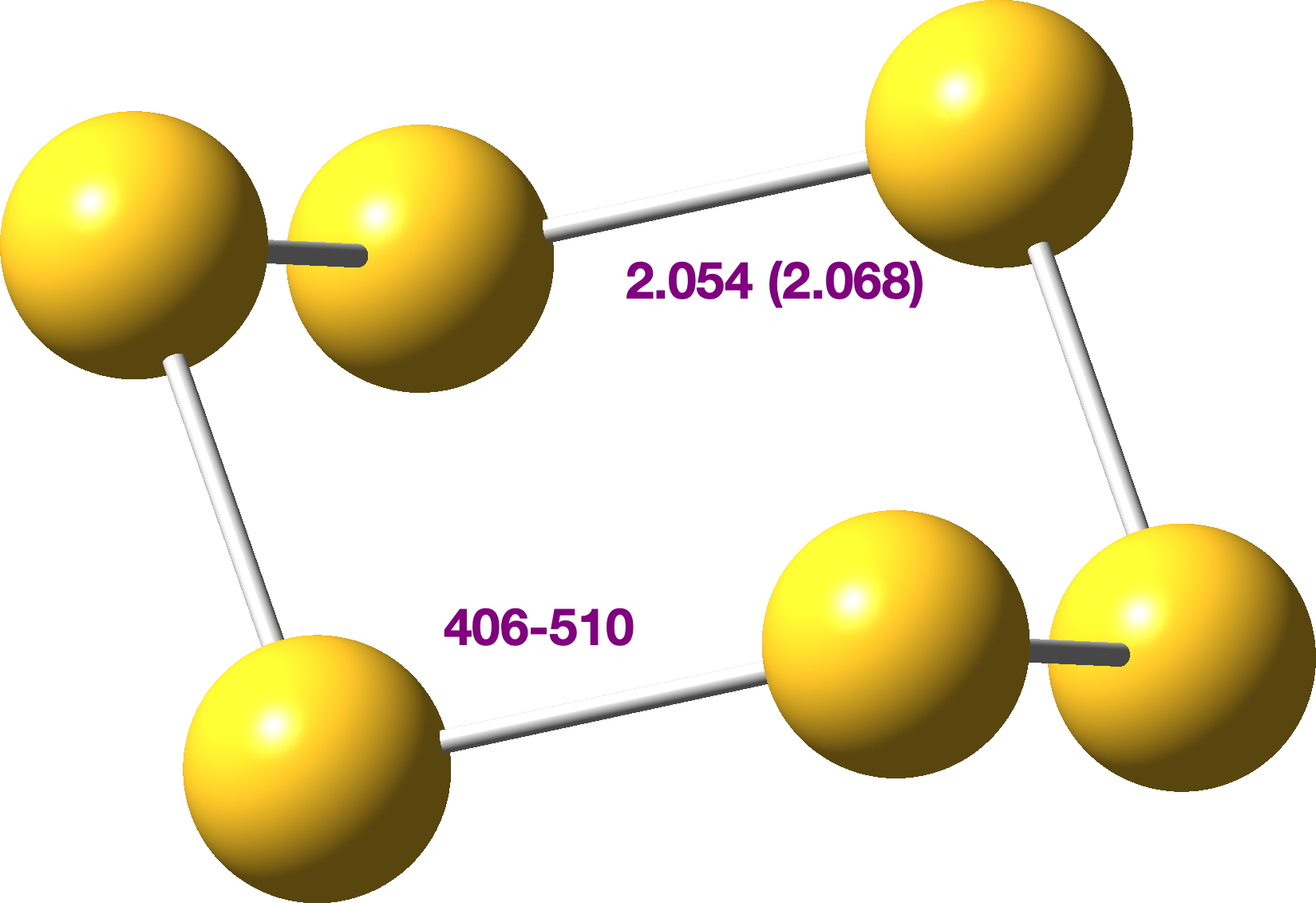
Since anomeric effects manifest in crystal structures by unequal bond lengths, at first sight it seemed unlikely that this ring could be shown to exhibit them. But wait, another conformation can be found, what in cyclohexane would be called the twist-boat. It is however around 12 kcal/mol higher in free energy than the stable form.[cite]10.14469/hpc/15260[/cite] and has lower (chiral) D2 symmetry. This now shows two slightly shorter bonds and four slightly longer bonds. The anomeric NBO E(2) perturbation energies are a relatively modest 7.93 kcal/mol (S1Lp-S2-S6σ*) resulting in modest S1-S2 bond shortening and comensurate S2-S6 lengthening. By symmetry, three other identical effects manifest.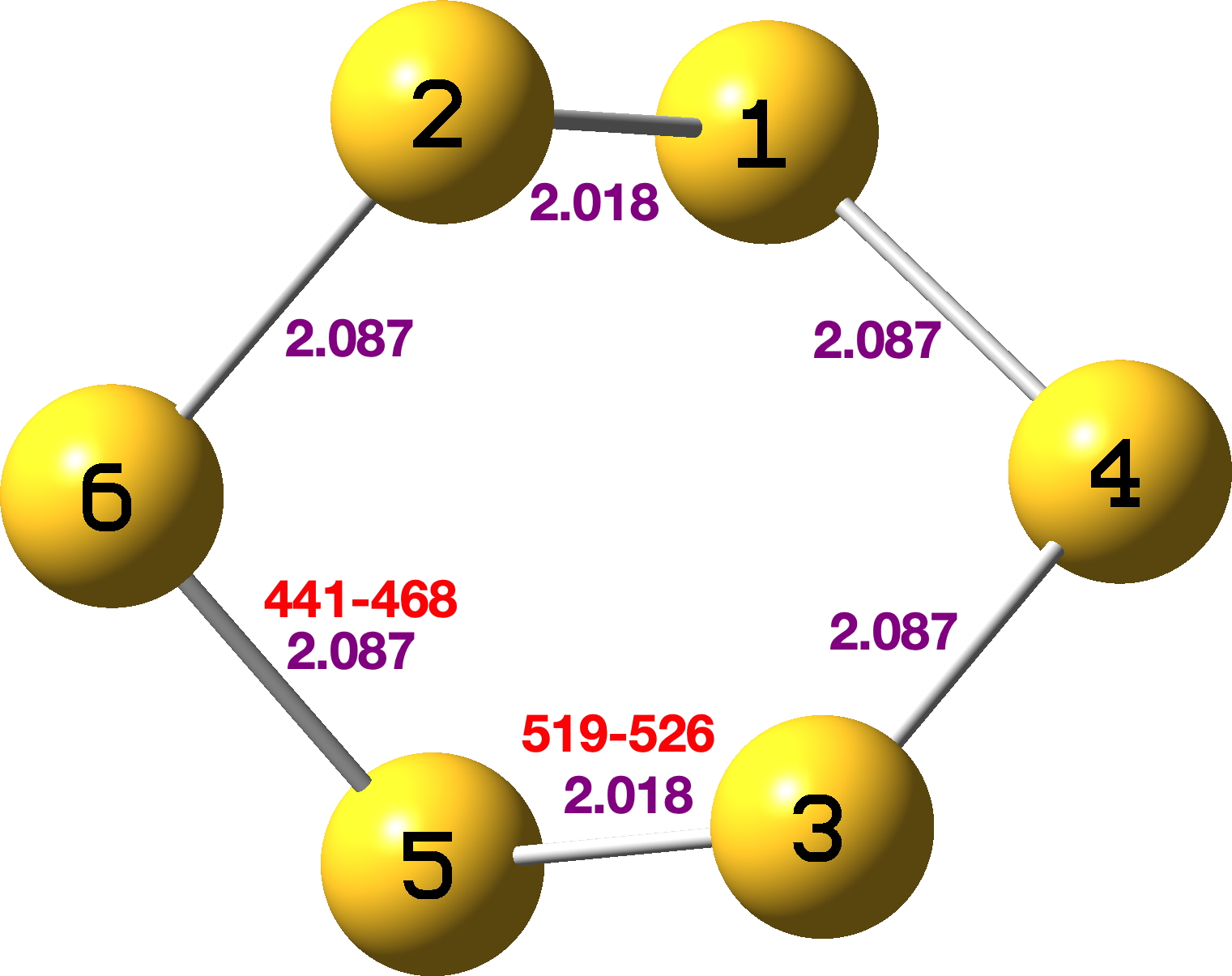
So these stereoelectronic effects CAN manifest in even-numbered rings, but only in this case as a higher energy conformer.
I also show O6, with C2 symmetry. As with O7 and O5 discussed previously[cite]10.59350/rzepa.28407[/cite] the anomeric effect promotes (partial) dissociation into three molecules of O2[cite]10.14469/hpc/15259[/cite], but this process is not complete (computationally) and weak partial bonds of ~1.997 and 2.06Å remain between the three O2 species, which are probably in fact artefacts of using a single-determinantal wavefunction. However it is fun to observe that the NBO E(2) terms are now (O1Lp-O5-O6σ*) 135 kcal/mol and the even larger (O2Lp-O3-O4σ*) 218 kcal/mol (tending to ∞ for a fully broken bond). These absurdly large values are a consequence of the non-converging perturbation expansion, but they are still amusing to see.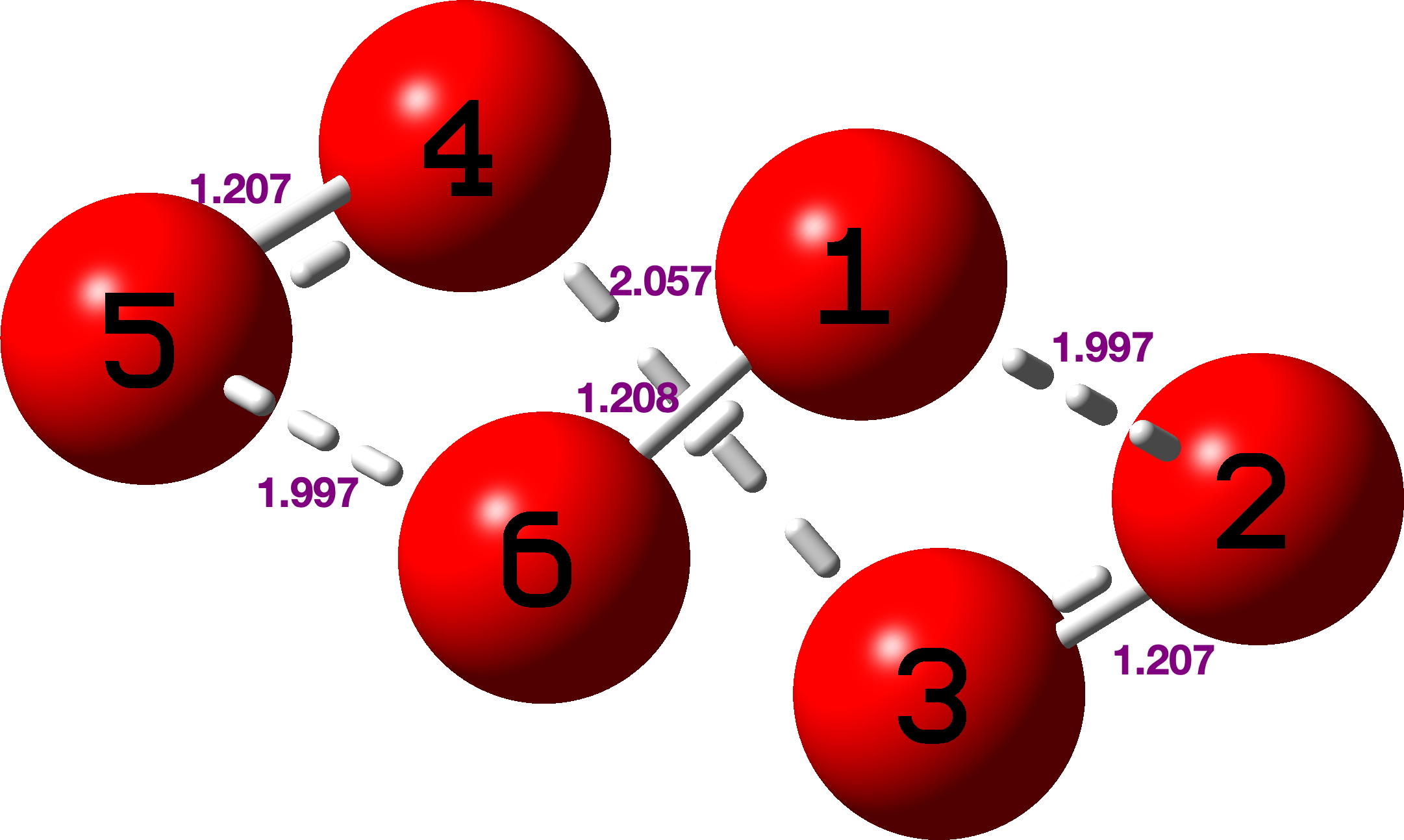
If you want to see the orbital interactions (as shown on the earlier blogs on this topic), why not download the wavefunction (the .fchk file) from the repository archive at the DOIs shown above and reveal them for yourself using suitable programs (the free Avogadro2 program is one that can do this exceedingly well). After this, I hesitate to say I will not find some other aspects of small sulfur and oxygen rings to write about, but other topics call for the time being!
Related
You can leave a response, or trackback from your own site.


1 Comment
85g0ux